题目内容
4.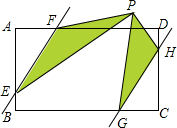 如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则图中阴影面积(△PEF和△PGH的面积和)等于( )
如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则图中阴影面积(△PEF和△PGH的面积和)等于( )| A. | 7 | B. | 8 | C. | 12 | D. | 14 |
分析 根据题目数据可以证明△AEF与△CGH全等,根据全等三角形对应边相等可得EF=GH,同理可得EG=FH,然后根据两组对边相等的四边形是平行四边形可得四边形EGHF是平行四边形,所以△PEF和△PGH的面积和等于平行四边形EGHF的面积的一半,再利用平行四边形EGHF的面积等于矩形ABCD的面积减去四周四个小直角三角形的面积即可求解.
解答 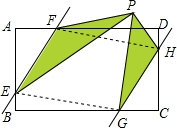 解:连接EG,FH,
解:连接EG,FH,
∵在矩形ABCD中,AD=6,AB=4,AF=CG=2,BE=DH=1,
∴AE=AB-BE=4-1=3,
CH=CD-DH=4-1=3,
∴AE=CH,
在△AEF与△CGH中,
$\left\{\begin{array}{l}{AE=CH}\\{∠A=∠C=90°}\\{AF=CG}\end{array}\right.$,
∴△AEF≌△CGH(SAS),
∴EF=GH,
同理可得,△BGE≌△DFH,
∴EG=FH,
∴四边形EGHF是平行四边形,
∵△PEF和△PGH的高的和等于点H到直线EF的距离,
∴△PEF和△PGH的面积和=$\frac{1}{2}$×平行四边形EGHF的面积,
平行四边形EGHF的面积
=4×6-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×(6-2)-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×(6-2),
=24-3-2-3-2,
=14,
∴△PEF和△PGH的面积和=$\frac{1}{2}$×14=7.
故选:A.
点评 本题考查了矩形的性质,平行四边形的判定与性质,作出辅助线并证明出四边形EGHF是平行四边形是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
15.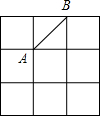 在边长为2的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为2的概率为( )
在边长为2的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为2的概率为( )
 在边长为2的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为2的概率为( )
在边长为2的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为2的概率为( )| A. | $\frac{3}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{5}{16}$ |
9.若反比例函数y=$\frac{k}{x}$的图象经过点(-3,2),则反比例函数y=-$\frac{k}{x}$的图象在( )
| A. | 一、二象限 | B. | 三、四象限 | C. | 一、三象限 | D. | 二、四象限 |
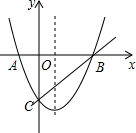 如图,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(-1,0),点C的坐标是(0,-3).
如图,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(-1,0),点C的坐标是(0,-3).