题目内容
3.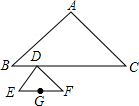 如图,点D是Rt△ABC斜边BC上一动点,以D为直角顶角作Rt△DEF,点G是EF中点,连接AG,若AB=AC=2,DE=DF=1.设AG=x,则x的最小值是$\frac{3\sqrt{2}}{2}$.
如图,点D是Rt△ABC斜边BC上一动点,以D为直角顶角作Rt△DEF,点G是EF中点,连接AG,若AB=AC=2,DE=DF=1.设AG=x,则x的最小值是$\frac{3\sqrt{2}}{2}$.
分析 当点D在BC中点时,利用等腰直角三角形的性质和勾股定理解答即可.
解答 解:当点D在BC中点时,
∵AB=AC=2,
∴BC=$2\sqrt{2}$,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}=\sqrt{{2}^{2}-(\sqrt{2})^{2}}=\sqrt{2}$,
∵DE=DF=1,
∴EF=$\sqrt{2}$,
∴DG=$\sqrt{D{E}^{2}-E{G}^{2}}=\sqrt{{1}^{2}-(\frac{\sqrt{2}}{2})^{2}}=\frac{\sqrt{2}}{2}$,
所以AG=$\frac{3\sqrt{2}}{2}$;
故答案为:$\frac{3\sqrt{2}}{2}$
点评 此题考查等腰直角三角形的性质,关键是根据用等腰直角三角形的性质和勾股定理解答.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
17.下面的命题是真命题的有( )
| A. | 有一组邻边相等的平行四边形是正方形 | |
| B. | 有一组邻边相等且有一角为直角的四边形为正方形 | |
| C. | 正方形是一组对边相等的矩形 | |
| D. | 正方形是有一个角为直角的菱形 |
15.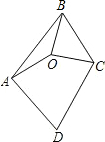 如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( )
如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( )
 如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( )
如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( )| A. | 70° | B. | 110° | C. | 140° | D. | 150° |
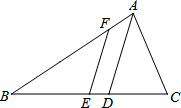 如图,在△ABC中,∠C=2∠B,AD平分∠BAC交BC于点D,点E为BC中点,EF∥AD交AB于点F.若BF=4AF,CD=$\frac{12}{5}$,则AC=$\frac{18}{5}$.
如图,在△ABC中,∠C=2∠B,AD平分∠BAC交BC于点D,点E为BC中点,EF∥AD交AB于点F.若BF=4AF,CD=$\frac{12}{5}$,则AC=$\frac{18}{5}$.