题目内容
11．
如图，?ABCD中，E是BC边的中点，已知△BEF的面积为S，则△ABF的面积为（ ）| A． | S | B． | 2S | C． | 3S | D． | 4S |
分析 由平行四边形ABCD中，E为BC的中点，可得△BEF∽△DAF，相似比为1：2，又由三角形的面积比其相似比，即可求得答案．
解答 解：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴△ADF∽△BEF，
∴$\frac{AD}{BE}$=$\frac{AF}{EF}$，
∵E是BC边的中点，
∴BE=$\frac{1}{2}$BC=$\frac{1}{2}$AD，
∴$\frac{AF}{EF}$=$\frac{1}{2}$，
∴$\frac{{S}_{△ABF}}{{S}_{△BEF}}$=$\frac{AF}{EF}$=$\frac{1}{2}$，
∵△BEF的面积为S，
∴△ABF的面积为2S，
故选B．
点评 此题考查了相似三角形的判定与性质与平行四边形的性质．此题难度不大，解题的关键是注意掌握相似三角形的面积比等于其相似比的平方定理的应用，注意数形结合思想的应用．
练习册系列答案
相关题目
如图，∠1+∠2=180°，∠3=∠B，那么∠EDG与∠DGB相等吗？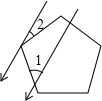
如图，一束平行太阳光照射到正五边形上，若∠1=45°，则∠2=27°．
如图，已知D是AC上一点，AB=DA，DE∥AB，∠B=∠DAE．求证：BC=AE．
直线AB经过点P（3，4）与坐标轴交于A、B，当S△AOB最小时，△AOB的内切圆半径是2．
20．为了反映某种股票的涨跌情况，应选择（ ）
| A． | 扇形统计图 | B． | 条形统计图 | C． | 折线统计图 | D． | 以上三种都一样 |