题目内容
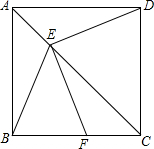 如图,正方形ABCD中,E为对角线AC上一点,连接BE、DE.F为BC上一点,且EF=EB.
如图,正方形ABCD中,E为对角线AC上一点,连接BE、DE.F为BC上一点,且EF=EB.(1)求证:EF⊥ED;
(2)若CF=AE,连接DF,求证:DF∥BE.
考点:正方形的性质,全等三角形的判定与性质,解直角三角形
专题:证明题
分析:(1)过E点作EM⊥BC并反向延长交AD于N,可证明△DEN≌△BME,再结合正方形的性质可证明∠DEF=90°,可证得结论;
(2)分别在Rt△BEM和Rt△DCF中计算∠EBM和∠DFC的正切值,可证明∠EBM=∠DFC,可证得平行.
(2)分别在Rt△BEM和Rt△DCF中计算∠EBM和∠DFC的正切值,可证明∠EBM=∠DFC,可证得平行.
解答: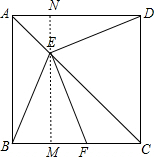 证明:(1)如图,过E点作EM⊥BC并反向延长交AD于N,
证明:(1)如图,过E点作EM⊥BC并反向延长交AD于N,
∵正方形ABCD关于AC对称,
∴DE=BE,
又∵AC平分∠BAD,∠DAE=45°,
∴△AEN为等腰直角三角形,
∴BM=AN=NE,
在Rt△DEN和Rt△BME中,
,
∴Rt△DEN≌Rt△BME(HL),
∴∠EDN=∠BEM,
∵BE=EF,EM⊥BF,
∴∠BEM=∠FEM,
∴∠EDN=∠FEM,
又∵∠NED+NDE=90°,
∴∠NED+∠MEF=90°,
∴∠DEF=90°,即DE⊥EF;
(2)设AN=BM=MF=1,则AE=CF=
,
∴BC=MN=2+
,
在Rt△BEM中,tan∠EBM=
=
=
+1,
在Rt△DCF中,tan∠DFC=
=
=
+1,
∴tan∠EBM=tan∠DFC,
∴∠EBM=∠DFC,
∴DF∥BE.
 证明:(1)如图,过E点作EM⊥BC并反向延长交AD于N,
证明:(1)如图,过E点作EM⊥BC并反向延长交AD于N,∵正方形ABCD关于AC对称,
∴DE=BE,
又∵AC平分∠BAD,∠DAE=45°,
∴△AEN为等腰直角三角形,
∴BM=AN=NE,
在Rt△DEN和Rt△BME中,
|
∴Rt△DEN≌Rt△BME(HL),
∴∠EDN=∠BEM,
∵BE=EF,EM⊥BF,
∴∠BEM=∠FEM,
∴∠EDN=∠FEM,
又∵∠NED+NDE=90°,
∴∠NED+∠MEF=90°,
∴∠DEF=90°,即DE⊥EF;
(2)设AN=BM=MF=1,则AE=CF=
| 2 |
∴BC=MN=2+
| 2 |
在Rt△BEM中,tan∠EBM=
| EM |
| BM |
| ||
| 1 |
| 2 |
在Rt△DCF中,tan∠DFC=
| DC |
| CF |
| ||
|
| 2 |
∴tan∠EBM=tan∠DFC,
∴∠EBM=∠DFC,
∴DF∥BE.
点评:本题主要考查正方形的性质和全等三角形的判定和性质及等腰三角形的性质,在(1)中构造三角形全等是解题的关键,注意利用等腰三角形的性质,在(2)中利用三角函数值相等可得到角相等是常用的方法.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
在平面直角坐标系xOy中有一点P(5,12),那么OP与x轴正半轴所夹的角的正弦值等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
将抛物线y=2x2向右平移1个单位,得到的抛物线是( )
| A、y=2x2+1 |
| B、y=2x2-1 |
| C、y=2(x+1) |
| D、y=2(x-1)2 |
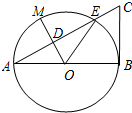 如图,以线段AB为直径的⊙O交线段AC于点E,点D是AE的中点,连接OD并延长交⊙O于点M,∠BOE=60°,cosC=
如图,以线段AB为直径的⊙O交线段AC于点E,点D是AE的中点,连接OD并延长交⊙O于点M,∠BOE=60°,cosC=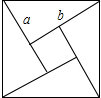 我国古代数学家赵给出的“弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是5,小正方形的面积是1,直角三角形的两只角边长分别是a,b,那么(a+b)2的值是
我国古代数学家赵给出的“弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是5,小正方形的面积是1,直角三角形的两只角边长分别是a,b,那么(a+b)2的值是