题目内容
3.已知a、b是一个等腰三角形的两边长,且满足a2+b2-4a-6b+13=0,求这个等腰三角形的周长.分析 先运用分组分解法进行因式分解,求出a,b的值,再代入求值即可.
解答 解:∵a2+b2-4a-6b+13=0,
∴(a2-4a+4)+(b2-6b+9)=0,
∴(a-2)2+(b-3)2=0,
∴a=2,b=3,
∴当腰为2时,等腰三角形的周长为2+2+3=7,
当腰为3时,等腰三角形的周长为2+3+3=8.
综上所述,该等腰三角形的周长为7或8.
点评 本题主要考查了因式分解及等腰三角形的性质,解题的关键是运用分组分解法进行因式分解.

练习册系列答案
相关题目
15.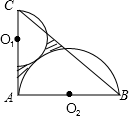 如图,△ABC是直角边长为6的等腰直角三角形,直角边AB是半圆O2的直径,半圆O1过C点且与半圆O2相切,则图中阴影部分的面积是( )
如图,△ABC是直角边长为6的等腰直角三角形,直角边AB是半圆O2的直径,半圆O1过C点且与半圆O2相切,则图中阴影部分的面积是( )
 如图,△ABC是直角边长为6的等腰直角三角形,直角边AB是半圆O2的直径,半圆O1过C点且与半圆O2相切,则图中阴影部分的面积是( )
如图,△ABC是直角边长为6的等腰直角三角形,直角边AB是半圆O2的直径,半圆O1过C点且与半圆O2相切,则图中阴影部分的面积是( )| A. | $\frac{46-13π}{4}$ | B. | $\frac{32-9π}{2}$ | C. | $\frac{23-13π}{4}$ | D. | $\frac{54-13π}{4}$ |
12.不等式2(1-x)>3的最大整数解是( )
| A. | 0 | B. | 1 | C. | -1 | D. | 无法确定 |
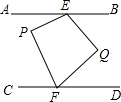 已知AB∥CD,P是AB、CD之间的一点,E、F分别是AB、CD上的定点,连接PE、PF,如图,在AB、CD之间另取一点Q,使∠PEQ=2∠BEQ,∠PFQ=2∠QFD,当∠P=∠Q时,判断PE、PF的位置关系,并说明理由.
已知AB∥CD,P是AB、CD之间的一点,E、F分别是AB、CD上的定点,连接PE、PF,如图,在AB、CD之间另取一点Q,使∠PEQ=2∠BEQ,∠PFQ=2∠QFD,当∠P=∠Q时,判断PE、PF的位置关系,并说明理由.