Question

13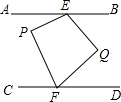．已知AB∥CD，P是AB、CD之间的一点，E、F分别是AB、CD上的定点，连接PE、PF，如图，在AB、CD之间另取一点Q，使∠PEQ=2∠BEQ，∠PFQ=2∠QFD，当∠P=∠Q时，判断PE、PF的位置关系，并说明理由．

Answer 1

分析 连接EF，根据平行线的性质得到∠BEF+∠EFD=180°，根据已知条件得到∠BEQ+∠QFD=180°-∠Q，由三角形的内角和得到∠1+∠2=180°-∠Q，于是得到∠P=∠Q=180°-∠1-∠2=90°，即可得到结论．

解答 解：PE⊥PF，
理由：连接EF，
∵AB∥CD，
∴∠BEF+∠EFD=180°，
∵∠PEQ+∠PFQ+∠P+∠Q=360°，∠P=∠Q，
∴∠PEQ+∠PFQ=360°-2∠Q，
∵∠PEQ=2∠BEQ，∠PFQ=2∠QFD，
∴2∠BEQ+2∠QFD=360°-2∠Q，
∴∠BEQ+∠QFD=180°-∠Q，
∵∠1+∠2=180°-∠Q，
∴∠BEQ+∠QFD=∠1+∠2=90°，
∴∠P=∠Q=180°-∠1-∠2=90°，
∴PE⊥PF．

点评 本题考查了平行线的性质，四边形的内角和，三角形的内角和，垂直的定义，连接EF，利用平行线的性质证明结论是解题的关键．