题目内容
（-x+2y）（-x-2y）等于_______；
x2-4y2
【解析】根据平方差公式可得：（-x+2y）（-x-2y）=x2-4y2.
练习册系列答案
相关题目
等腰△ABC中，AB=AC，一边上的中线BD将这个三角形的周长分为15和12两个部分，则这个等腰三角形的底边长为（ ）
A. 7 B. 11 C. 7或11 D. 7或10
C
【解析】试题分析：题中给出了周长关系，要求底边长，首先应先想到等腰三角形的两腰相等，寻找问题中的等量关系，列方程求解，然后结合三角形三边关系验证答案．设等腰三角形的底边长为x，腰长为y，则根据题意，得①或②，解方程组①得：x=11，y=8，根据三角形三边关系定理，此时能组成三角形；解方程组②得：x=7，y=10，根据三角形三边关系定理此时能组成三角形，即等腰三角形的底边长是11或7.
... 982+（a-b）2
9604+a2-2ab+b2
【解析】试题分析：把98化为（100-2），利用完全平方公式即可解答.
试题解析：
982+（a-b）2=（100-2）2+a2-2ab+b2=10000-400+4+a2-2ab+b2=9604+a2-2ab+b2. （x+5y）2 等于（ ）
A. x2-5y 2 B. x2-10y+5y 2 C. x2+10xy+25y 2 D. x2-y+25y 2
C
【解析】根据完全平方公式可得：（x+5y）2=x2+10xy+25y 2 ，故选C. （3a-b）（3a+b）-（a2+b2）
8a2-2b2
【解析】试题分析：先根据平方差公式计算，再合并同类项即可.
试题解析：
（3a-b）（3a+b）-（a2+b2）=9a2-b2-a2-b2=8a2-2b2. [c+（a2)2][c-（a2)2]等于（ ）
A. c -a2 B. c2 -a8 C. c2 -a2 D. c2 -a4
B
【解析】根据平方差公式和幂的乘方法则可得：[c+（a2)2][c-（a2)2]= =c2 -a8，故选B. （2x+y 2 ）（2x-y 2 ）等于（ ）
A. x2-y 4 B. x2-y 2 C. 4x2-y4 D. 4x2-y 2
C
【解析】根据平方差公式可得：（2x+y 2 ）（2x-y 2 ）=4x2-y4 ，故选C. 已知点M（2m -3,8），N（m -1,-3），且MN//y轴，则m=________.
2
【解析】由MN//y轴，可得点M、N的横坐标相同，即2m-3=m-1，解得m=2. 分式的概念：对于式子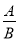
，如果除式B中含有_____，那么称
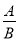为分式，其中A称为分式的____，B称为分式的_____.
字母 分子 分母
【解析】利用分式的概念即可得出答案.
【解析】
对于式子，如果除式B中含有字母，那么称为分式，其中A称为分式的分子，B称为分式的他、分母.
故答案为：字母；分子；分母.