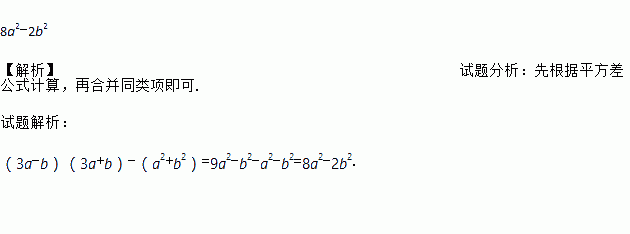题目内容
(3a-b)(3a+b)-(a2+b2)
 8a2-2b2
【解析】试题分析:先根据平方差公式计算,再合并同类项即可.
试题解析:
(3a-b)(3a+b)-(a2+b2)=9a2-b2-a2-b2=8a2-2b2.
8a2-2b2
【解析】试题分析:先根据平方差公式计算,再合并同类项即可.
试题解析:
(3a-b)(3a+b)-(a2+b2)=9a2-b2-a2-b2=8a2-2b2.
练习册系列答案
相关题目
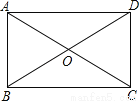
如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是
A.8 B.6 C.4 D.2
 C
【解析】
试题分析:∵四边形ABCD是矩形,∴AO=BO=CO=DO。
∴△ABO,△BCO,△DCO,△ADO都是等腰三角形。
故选C。
C
【解析】
试题分析:∵四边形ABCD是矩形,∴AO=BO=CO=DO。
∴△ABO,△BCO,△DCO,△ADO都是等腰三角形。
故选C。 如果函数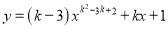 是二次函数,那么
是二次函数,那么 的值一定是( )
的值一定是( )
A. 0 B. 3 C. 0或3 D. 1或2
 A
【解析】试题分析:根据二次函数的定义,得:
k2-3k+2=2,
解得k=0或k=3;
又∵k-3≠0,
∴k≠3.
∴当k=0时,这个函数是二次函数.
故选A.
A
【解析】试题分析:根据二次函数的定义,得:
k2-3k+2=2,
解得k=0或k=3;
又∵k-3≠0,
∴k≠3.
∴当k=0时,这个函数是二次函数.
故选A. (3z-y)2 等于( )
A. 9z2-y+y2 B. 9z2-yz+y2 C. 9z2-6yz+y2 D. 3z2-6yz+y2
 C
【解析】根据完全平方公式可得:(3z-y)2 =9z2-6yz+y2,故选C.
C
【解析】根据完全平方公式可得:(3z-y)2 =9z2-6yz+y2,故选C. (x+5y)2 等于( )
A. x2-5y 2 B. x2-10y+5y 2 C. x2+10xy+25y 2 D. x2-y+25y 2
 C
【解析】根据完全平方公式可得:(x+5y)2=x2+10xy+25y 2 ,故选C.
C
【解析】根据完全平方公式可得:(x+5y)2=x2+10xy+25y 2 ,故选C. (-x+2y)(-x-2y)等于_______;
 x2-4y2
【解析】根据平方差公式可得:(-x+2y)(-x-2y)=x2-4y2.
x2-4y2
【解析】根据平方差公式可得:(-x+2y)(-x-2y)=x2-4y2. (x+3ab)(x-3ab)等于( )
A. x2 -9a2b2 B. x2 -9ab2 C. x2 -ab2 D. x2 -a2b2
 A
【解析】根据平方差公式可得:(x+3ab)(x-3ab)=x2 -9a2b2,故选A.
A
【解析】根据平方差公式可得:(x+3ab)(x-3ab)=x2 -9a2b2,故选A. 解下列不等式组并把解在数轴上表示出来.
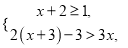
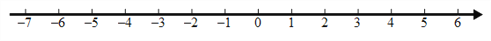
 ,在数轴上表示见解析.
【解析】试题分析:分别求出两个不等式的解集,这两个不等式解集的公共部分即为不等式组的解集,在数轴上表示出来即可.
试题解析:
由(1)得,
由(2)得,
不等式组的解集在数轴上表示如下:
,在数轴上表示见解析.
【解析】试题分析:分别求出两个不等式的解集,这两个不等式解集的公共部分即为不等式组的解集,在数轴上表示出来即可.
试题解析:
由(1)得,
由(2)得,
不等式组的解集在数轴上表示如下: 分式 的值为0,则( ).
的值为0,则( ).
A.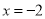 B.
B.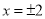 C.
C.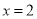 D.
D.
 C
【解析】
试题分析:根据分式的值为0的条件为分母=0,分子≠0,因此可求-4=(x+2)(x-2)=0,解得x=-2或,x=2,而x+2≠0,即x≠-2,所以x=2.
故选C
C
【解析】
试题分析:根据分式的值为0的条件为分母=0,分子≠0,因此可求-4=(x+2)(x-2)=0,解得x=-2或,x=2,而x+2≠0,即x≠-2,所以x=2.
故选C