题目内容
7. 如图,已知P是边长为1的正三角形ABC内的一个动点,如PE⊥AB于E,PF⊥BC于F,PD⊥AC于D,则PD+PE+PF的值为$\frac{\sqrt{3}}{2}$.
如图,已知P是边长为1的正三角形ABC内的一个动点,如PE⊥AB于E,PF⊥BC于F,PD⊥AC于D,则PD+PE+PF的值为$\frac{\sqrt{3}}{2}$.
分析 连接PA、PB、PC利用等面积的知识可求出PD+PE+PF的和的值.
解答  解:连接PA、PB、PC,
解:连接PA、PB、PC,
∵△ABC是边长为1的正三角形,
∴可得三角形ABC的面积为$\frac{\sqrt{3}}{4}$,
SABC=SAPB+SAPC+SBPC=$\frac{1}{2}$×1×PE+$\frac{1}{2}$×1×PF+$\frac{1}{2}$×1×PD=$\frac{1}{2}$(PD+PE+PF),
∴可得PD+PE+PF=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$
点评 本题考查了等边三角形的性质,难度不大,解决本题的关键是利用等面积法确定答案.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
18.某土特产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售.按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,解答以下问题:
(1)设装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,求y与x之间的函数关系式;
(2)如果装运每种土特产的车辆都不少于3辆,求出此次销售最大利润的值.
| 土特产品种 | 甲 | 乙 | 丙 |
| 每辆汽车运载量(吨) | 8 | 6 | 5 |
| 每吨土特产获利(百元) | 12 | 16 | 10 |
(2)如果装运每种土特产的车辆都不少于3辆,求出此次销售最大利润的值.
2.已知直角三角形的两条直角边分别为3cm和4cm,则斜边上的中线等于( )
| A. | 2cm | B. | 2.4cm | C. | 2.5cm | D. | 3cm |
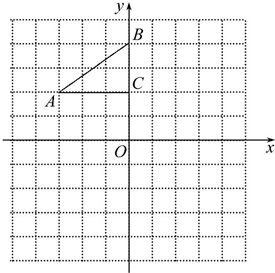 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2). 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(-2,-5 ),C (5,n),交y轴于点B,交x轴于点D,那么不等式kx+b-$\frac{m}{x}$>0的解集是-2<x<0或x>5.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(-2,-5 ),C (5,n),交y轴于点B,交x轴于点D,那么不等式kx+b-$\frac{m}{x}$>0的解集是-2<x<0或x>5. 如图,矩形EFGH内接于△ABC,且边FG落在BC上,AD⊥BC,BC=3cm,AD=2cm,EF=$\frac{2}{3}$EH,求EH的长.
如图,矩形EFGH内接于△ABC,且边FG落在BC上,AD⊥BC,BC=3cm,AD=2cm,EF=$\frac{2}{3}$EH,求EH的长.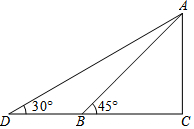 如图所示,某幼儿园为加强安全管理,决定将园内滑滑板的倾斜角由45°降为30°,已知原滑滑板AB的长为4米,点D,B,C在同一水平地面上.
如图所示,某幼儿园为加强安全管理,决定将园内滑滑板的倾斜角由45°降为30°,已知原滑滑板AB的长为4米,点D,B,C在同一水平地面上. 如图,已知平面直角坐标系中,直线AB与x轴交于点A(3,0),与反比例函数在第三象限内的图象交于点B(-1,a),连接BO,若S△AOB=3.
如图,已知平面直角坐标系中,直线AB与x轴交于点A(3,0),与反比例函数在第三象限内的图象交于点B(-1,a),连接BO,若S△AOB=3.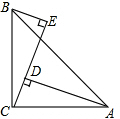 如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE于D,BE⊥CE于E.
如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE于D,BE⊥CE于E.