题目内容
8.计算题(1)5$\sqrt{2}$+$\sqrt{8}$-7$\sqrt{18}$;
( 2)$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$-$\sqrt{24}$;
(3)$\sqrt{18a}$-$\sqrt{\frac{1}{8}a}$+4$\sqrt{0.5a}$;
(4)(3+$\sqrt{5}$)(3-$\sqrt{5}$)-($\sqrt{3}$-1)2.
分析 (1)先把各二次根式化简为最简二次根式,然后合并即;
(2)先进行二次根式的乘除法运算,然后化简后合并即可;
(3)先把各二次根式化简为最简二次根式,然后合并即;
(4)利用平方差公式和完全平方公式计算.
解答 解:(1)原式=5$\sqrt{2}$+2$\sqrt{2}$-21$\sqrt{2}$
=-14$\sqrt{2}$;
(2)原式=$\sqrt{48÷3}$-$\sqrt{\frac{1}{2}×12}$-2$\sqrt{6}$
=4-$\sqrt{6}$+2$\sqrt{6}$
=4+$\sqrt{6}$;
(3)原式=3$\sqrt{2a}$-$\frac{\sqrt{2a}}{4}$+2$\sqrt{2a}$
=$\frac{23\sqrt{2a}}{4}$;
(4)原式=9-5-(3-2$\sqrt{3}$+1)
=4-4+2$\sqrt{3}$
=2$\sqrt{3}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
相关题目
18.x的$\frac{1}{3}$相当于y的$\frac{1}{8}$(x不等于0),则x、y的关系是( )
| A. | x>y | B. | x<y | C. | x=y | D. | 无法比较 |
16.下列等式成立的是( )
| A. | $\frac{1}{a}+\frac{2}{b}=\frac{3}{a+b}$ | B. | $\frac{ab}{{ab-{b^2}}}=\frac{a}{a-b}$ | C. | $\frac{2}{2a+b}=\frac{1}{a+b}$ | D. | $\frac{a}{-a+b}=-\frac{a}{a+b}$ |
20.下列命题是真命题的是( )
| A. | 垂线段最短 | |
| B. | 垂直于同一条直线的两直线平行 | |
| C. | 过一点有且只有一条直线与已知直线平行 | |
| D. | 两条直线不平行则相交 |
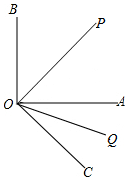 如图,∠AOB是直角,OP平分∠AOB,OQ平分∠AOC,∠POQ=70°,求∠AOC的度数.
如图,∠AOB是直角,OP平分∠AOB,OQ平分∠AOC,∠POQ=70°,求∠AOC的度数.