题目内容
19.方程组$\left\{\begin{array}{l}{x+y+z=10}\\{x+y=8}\\{x=y+z}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=5}\\{y=3}\\{z=2}\end{array}\right.$.分析 将方程组第三个方程代入第一个方程求出x的值,把x的值代入第二个方程求出y的值,进而求出z的值,即可确定出方程组的解.
解答 解:$\left\{\begin{array}{l}{x+y+z=10①}\\{x+y=8②}\\{x=y+z③}\end{array}\right.$,
把③代入①得:2x=10,即x=5,
把x=5代入①得:y=3,
把x=5,y=3代入①得:z=2,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=3}\\{z=2}\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{x=5}\\{y=3}\\{z=2}\end{array}\right.$
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
7.我国“天河二号”计算机的运算速度世界最快,若完成一次基本运算的时间约为0.000 000 000 001s,把这个数用科学记数法可表示为( )
| A. | 0.1×10-11s | B. | 0.1×10-12s | C. | 1×10-11s | D. | 1×10-12s |
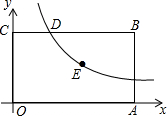 如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形的对称中心E,且与边BC交于点D,则点CD的长为1.
如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形的对称中心E,且与边BC交于点D,则点CD的长为1.
 如图,在△ABC中,D,E两点分别在边AB,AC上,AB=8cm,AC=6cm,AD=3cm,要使△ADE与△ABC相似,则线段AE的长为4或$\frac{9}{4}$cm.
如图,在△ABC中,D,E两点分别在边AB,AC上,AB=8cm,AC=6cm,AD=3cm,要使△ADE与△ABC相似,则线段AE的长为4或$\frac{9}{4}$cm.