题目内容
11.在?ABCD中,边AB=3,对角线AC=2$\sqrt{5}$,BD=4,则?ABCD的面积等于4$\sqrt{5}$.分析 设?ABCD的对角线AC和BD交于点O,由AC,BD的长易求得OA与OB的长,又由勾股定理的逆定理,证得AC⊥BD,继而求得答案.
解答 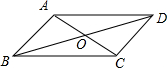 解:∵四边形ABCD是平行四边形,且AC=2$\sqrt{5}$,BD=4,
解:∵四边形ABCD是平行四边形,且AC=2$\sqrt{5}$,BD=4,
∴OA=OC=$\frac{1}{2}$AC=$\sqrt{5}$,OB=OD=2,
∵AB=3,
∴OA2+OB2=AB2,
∴△OAB是直角三角形,且∠AOB=90°,
即AC⊥BD,
∴?ABCD面积为:$\frac{1}{2}$BD•AC=4×2$\sqrt{5}$=4$\sqrt{5}$.
故答案为:4$\sqrt{5}$.
点评 此题考查了平行四边形的性质与勾股定理的逆定理.此题难度不大,熟练掌握平行四边形的各种性质是解题关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
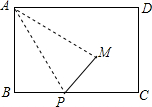 (背景)某班在一次数学实践活动中,对矩形纸片进行折叠实践操作,并将其产生的数学问题进行相关探究.
(背景)某班在一次数学实践活动中,对矩形纸片进行折叠实践操作,并将其产生的数学问题进行相关探究.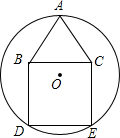 已知,如图等边三角形ABC和正方形BDEC的边长均为2,⊙O经过点A,D,E三点.
已知,如图等边三角形ABC和正方形BDEC的边长均为2,⊙O经过点A,D,E三点. 如图,矩形ABCD的对角线AC、BD相交于点0,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为6,则cos∠BOE=$\frac{2}{3}$.
如图,矩形ABCD的对角线AC、BD相交于点0,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为6,则cos∠BOE=$\frac{2}{3}$.