题目内容
8.已知y=y1-y2,y1与x成正比例函数,y2与x+3成反比例,当x=0时,y=3;当x=3时,y=0,求y与x的函数关系式,并指出自变量的取值范围.分析 根据题意分别设出y1,y2,代入y=y1-y2,表示出y与x的解析式,将已知两对值代入求出k与b的值,确定出解析式.
解答 解:根据题意设y1=kx,y2=$\frac{b}{x+3}$,即y=y1-y2=kx-$\frac{b}{x+3}$,
将x=0时,y=3;当x=3时,y=0分别代入得:$\left\{\begin{array}{l}{-\frac{b}{3}=3}\\{3k-\frac{b}{6}=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-9}\end{array}\right.$,
则y=-$\frac{1}{2}$x+$\frac{9}{x+3}$(x≠-3).
点评 本题考查了待定系数法求反比例函数的解析式:设反比例函数的解析式为y=$\frac{k}{x}$(k≠0),再把反比例函数图象上的一个点的坐标代入得到关于k的方程,解方程求出k的值,从而确定反比例函数的解析式.

练习册系列答案
相关题目
18.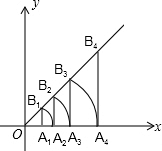 如图,平面坐标系内,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…按此作法进行去,点Bn(n为正整数)的横坐标为( )
如图,平面坐标系内,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…按此作法进行去,点Bn(n为正整数)的横坐标为( )
 如图,平面坐标系内,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…按此作法进行去,点Bn(n为正整数)的横坐标为( )
如图,平面坐标系内,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…按此作法进行去,点Bn(n为正整数)的横坐标为( )| A. | ($\sqrt{2}$)n-1 | B. | ($\sqrt{2}$)n | C. | ($\sqrt{2}$)n+1 | D. | 2n |
13.反比例函数y=$\frac{k}{x}$的图象经过点A(-2,-5),则当1<x<2时,y的取值范围是( )
| A. | -10<y<-5 | B. | -2<y<-1 | C. | 5<y<10 | D. | y>10 |
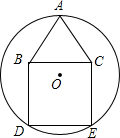 已知,如图等边三角形ABC和正方形BDEC的边长均为2,⊙O经过点A,D,E三点.
已知,如图等边三角形ABC和正方形BDEC的边长均为2,⊙O经过点A,D,E三点.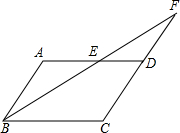 如图,在?ABCD中,AB=4,AD=7,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF的长是( )
如图,在?ABCD中,AB=4,AD=7,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF的长是( )