题目内容
3.⊙O1过半径为3cm的⊙O2的圆心O2,圆O1的弦AB切⊙O2于点C,AO2=15,BO2=4,求⊙O1的半径.分析 根据题意画出图形,进而利用切线的性质得出CO2的长,再利用垂径定理以及相交弦定理、勾股定理得出⊙O1的半径.
解答 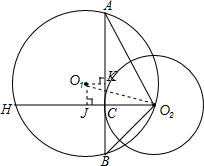 解:如图所示:连接O2C,并延长交⊙O1于点H,作O1J⊥O2H于点J,O1K⊥AB于点K,
解:如图所示:连接O2C,并延长交⊙O1于点H,作O1J⊥O2H于点J,O1K⊥AB于点K,
∵⊙O2的半径为3cm,
∴CO2=3cm,
∵AO2=15,BO2=4,
∴AC=$\sqrt{{O}_{2}{A}^{2}-{O}_{2}{C}^{2}}$=6$\sqrt{6}$(cm),
BC=$\sqrt{{O}_{2}{B}^{2}-{O}_{2}{C}^{2}}$=$\sqrt{7}$(cm),
∵AC•BC=HC•CO2,
∴HC=$\frac{6\sqrt{6}×\sqrt{7}}{3}$=2$\sqrt{42}$(cm),
O1J=KB-CB=$\frac{1}{2}$(6$\sqrt{6}$+$\sqrt{7}$)-$\sqrt{7}$=(3$\sqrt{6}$-$\frac{\sqrt{7}}{2}$)cm,
JO2=$\frac{1}{2}$(2$\sqrt{42}$+3)=($\sqrt{42}$+$\frac{3}{2}$)cm,
∴O1O2=$\sqrt{{O}_{1}{J}^{2}+{O}_{2}{J}^{2}}$=10(cm),
故⊙O1的半径为10cm.
点评 此题主要考查了切线的性质、垂径定理以及相交弦定理、勾股定理等知识,正确得出HC的长是解题关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
13.若x<1,那么$\sqrt{(x-1)^{2}}$+|5-x|等于( )
| A. | 6-2x | B. | 2x-6 | C. | 4 | D. | -4 |
15.一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元. 每辆车的月租金定为多少元时,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
| x | 4500 | 4000 | 3800 | 3200 |
| y | 70 | 80 | 84 | 96 |
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元. 每辆车的月租金定为多少元时,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
12.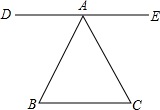 茗茗和墨墨一起做游戏,茗茗过三角形ABC的顶点A画了一条直线DE,如图所示,墨墨说:“直线DE与BC平行.”茗茗问:“你是怎么知道的?”墨墨回答:“我用量角器测量了下,发现□与□相等.”( )
茗茗和墨墨一起做游戏,茗茗过三角形ABC的顶点A画了一条直线DE,如图所示,墨墨说:“直线DE与BC平行.”茗茗问:“你是怎么知道的?”墨墨回答:“我用量角器测量了下,发现□与□相等.”( )
 茗茗和墨墨一起做游戏,茗茗过三角形ABC的顶点A画了一条直线DE,如图所示,墨墨说:“直线DE与BC平行.”茗茗问:“你是怎么知道的?”墨墨回答:“我用量角器测量了下,发现□与□相等.”( )
茗茗和墨墨一起做游戏,茗茗过三角形ABC的顶点A画了一条直线DE,如图所示,墨墨说:“直线DE与BC平行.”茗茗问:“你是怎么知道的?”墨墨回答:“我用量角器测量了下,发现□与□相等.”( )| A. | ∠DAB,∠B | B. | ∠DAB,∠C | C. | ∠EAC,∠B | D. | ∠DAB,∠EAC |
 如图,已知DB∥FG∥EC,∠ABD=60°,∠ACE=60°,AP是∠BAC的平分线,求∠PAG的度数.
如图,已知DB∥FG∥EC,∠ABD=60°,∠ACE=60°,AP是∠BAC的平分线,求∠PAG的度数.