题目内容
14.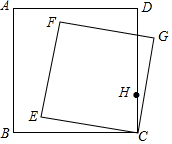 如图,正方形ABCD中,AB=4,点H在CD边上,且CH=1,点E绕点B旋转,同时,以CE为边在BC上方作正方形CEFG,在点E运动过程中,当线段FH取得最小值时,∠CBE的正切为( )
如图,正方形ABCD中,AB=4,点H在CD边上,且CH=1,点E绕点B旋转,同时,以CE为边在BC上方作正方形CEFG,在点E运动过程中,当线段FH取得最小值时,∠CBE的正切为( )| A. | $\frac{1}{5}$ | B. | $\frac{\sqrt{2}}{5}$ | C. | $\frac{\sqrt{2}}{7}$ | D. | $\frac{1}{7}$ |
分析 先根据△ACF∽△BCE,确定点F的运动路径为以A为圆心,以$\sqrt{2}$BE长为半径的圆,再连接AF,FH,AH,根据AH≤AF+FH,而AH和AF的长度不变,可得当点F在线段AH上时,FH=AH-AF(最短),过H作HQ⊥AC于Q,求得HQ和AQ的长,即可得到tan∠CBE=tan∠QAH=$\frac{HQ}{AQ}$=$\frac{1}{7}$,进而得出∠CBE的正切值.
解答 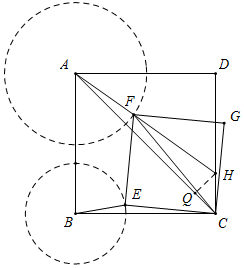 解:如图所示,点E绕点B旋转时,其路径为以B为圆心,BE长为半径的圆,
解:如图所示,点E绕点B旋转时,其路径为以B为圆心,BE长为半径的圆,
连接AC,AF,FC,则∠ACB=∠FCE=45°,
∴∠ACF=∠BCE,
∵AC=$\sqrt{2}$BC,FC=$\sqrt{2}$CE,
∴$\frac{AC}{BC}$=$\frac{FC}{EC}$=$\sqrt{2}$,
∴△ACF∽△BCE,
∴$\frac{AF}{BE}$=$\frac{AC}{BC}$=$\sqrt{2}$,
即AF=$\sqrt{2}$BE,
∴点E绕点B旋转时,点F的运动路径为以A为圆心,以$\sqrt{2}$BE长为半径的圆,
连接AF,FH,AH,
∵AH≤AF+FH,而AH和AF的长度不变,
∴当点F在线段AH上时,FH=AH-AF(最短),
此时,由相似三角形的性质可得∠CBE=∠CAH,
过H作HQ⊥AC于Q,则△CHQ是等腰直角三角形,
∵CH=1,
∴HQ=CQ=$\frac{\sqrt{2}}{2}$,
又∵等腰Rt△ABC中,AC=$\sqrt{2}$AB=4$\sqrt{2}$,
∴AQ=$\frac{7}{2}\sqrt{2}$,
∴tan∠CBE=tan∠QAH=$\frac{HQ}{AQ}$=$\frac{\frac{1}{2}\sqrt{2}}{\frac{7}{2}\sqrt{2}}$=$\frac{1}{7}$,即∠CBE的正切值为$\frac{1}{7}$.
故选:D.
点评 本题主要考查了旋转的性质,正方形的性质,等腰直角三角形的性质,解直角三角形以及相似三角形的判定与性质的综合应用,解决问题的关键是作辅助线构造直角三角形以及相似三角形,依据相似三角形的对应边成比例得到点F的运动轨迹.解题时注意:两边对应成比例且夹角相等的两个三角形相似.

 名校课堂系列答案
名校课堂系列答案| A. | 30°,75° | B. | 40°,95° | C. | 50°,115° | D. | 55°,125° |
| A. | -$\frac{10}{3}$a>-$\frac{10}{3}$b | B. | a2>b2 | C. | $\frac{3}{a}$>$\frac{3}{b}$ | D. | -$\frac{1}{5}$+a>-$\frac{1}{5}$+b |
| A. | $\sqrt{\frac{a}{2{b}^{2}}}$=$\frac{1}{2b}$$\sqrt{a}$(b>0) | B. | $\sqrt{\frac{7x}{12{y}^{3}}}$=$\frac{1}{6{y}^{2}}$$\sqrt{21xy}$ | ||
| C. | $\sqrt{{a}^{2}+{b}^{2}}$=a+b(a≥0,b≥0) | D. | 5$\sqrt{\frac{2a}{5}}$=$\sqrt{2a}$ |
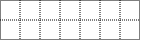 如图是小明家沙发坐垫的平面示意图,中间的双人沙发坐垫面积为2×3(单位面积),左右两边的是坐垫面积为2×2(单位面积)的单人沙发,小明和小虎在玩“藏密码”的游戏,已知小虎将密码藏在沙发坐垫下,则密码藏在单人沙发坐垫下的概率是( )
如图是小明家沙发坐垫的平面示意图,中间的双人沙发坐垫面积为2×3(单位面积),左右两边的是坐垫面积为2×2(单位面积)的单人沙发,小明和小虎在玩“藏密码”的游戏,已知小虎将密码藏在沙发坐垫下,则密码藏在单人沙发坐垫下的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A2旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至得C13,若P(38,m)在第13段抛物线C13上,则m=2.
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A2旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至得C13,若P(38,m)在第13段抛物线C13上,则m=2. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论: 如图,在直角坐标系中,A、B的坐标分别为(4,0),(0,2),将线段AB向上平移m个单位得到A′B′,如果△OA′B′为等腰三角形,那么m的值为2或3或2$\sqrt{5}$-2.
如图,在直角坐标系中,A、B的坐标分别为(4,0),(0,2),将线段AB向上平移m个单位得到A′B′,如果△OA′B′为等腰三角形,那么m的值为2或3或2$\sqrt{5}$-2.