题目内容
4.(1)先化简,再求值:($\frac{2}{a+1}$+$\frac{a+2}{{a}^{2}-1}$)÷$\frac{a}{a-1}$,其中a=$\sqrt{2}$-1.(2)已知关于x,y的二元一次方程$\left\{\begin{array}{l}{2x-y=2m}\\{x+3y=m-1}\end{array}\right.$的解满足x<y,求m的取值范围.
分析 (1)先将括号内通分,计算加法、同时将除法转化为乘法,再约分即可得;
(2)先将m看做已知的常数解方程组,再根据x<y得出关于m的不等式,解之可得.
解答 解:(1)原式=[$\frac{2}{a+1}$+$\frac{a+2}{(a+1)(a-1)}$]•$\frac{a-1}{a}$
=$\frac{2(a-1)+(a+2)}{(a+1)(a-1)}$•$\frac{a-1}{a}$
=$\frac{3a}{(a+1)(a-1)}$•$\frac{a-1}{a}$
=$\frac{3}{a+1}$,
当a=$\sqrt{2}$-1时,原式=$\frac{3}{\sqrt{2}-1+1}$=$\frac{3\sqrt{2}}{2}$;
(2)解方程组$\left\{\begin{array}{l}{2x-y=2m}\\{x+3y=m-1}\end{array}\right.$得:$\left\{\begin{array}{l}{x=m-\frac{1}{7}}\\{y=-\frac{2}{7}}\end{array}\right.$,
∵x<y,
∴m-$\frac{1}{7}$<-$\frac{2}{7}$,
解得:m<-$\frac{1}{7}$.
点评 本题主要考查分式的化简求值及解方程组和不等式的能力,熟练掌握分式的混合运算顺序及法则和解方程、不等式的基本步骤和依据是解题的关键.

练习册系列答案
相关题目
12.已知a是一个一位数,b是一个两位数,若将a放在b的左边,那么所成的三位数是( )
| A. | 10(a+b) | B. | ab | C. | 100a+10b | D. | 100a+b |
19.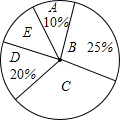 近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计扇形图.
近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计扇形图.
(1)求出本次被调查的学生数;
(2)请求出统计表中a的值;
(3)求每天体育锻炼时间不小于100分钟学生人数的百分比所占扇形的圆心角度数;
(4)根据调查结果,请你估计该校2400名学生中每天体育锻炼时间不少于1小时的学生人数.
 近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计扇形图.
近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计扇形图.| 组别 | A | B | C | D | E |
| 时间t(分钟) | t<40 | 40≤t<60 | 60≤t<80 | 80≤t<100 | t≥100 |
| 人数 | 12 | 30 | a | 24 | 12 |
(2)请求出统计表中a的值;
(3)求每天体育锻炼时间不小于100分钟学生人数的百分比所占扇形的圆心角度数;
(4)根据调查结果,请你估计该校2400名学生中每天体育锻炼时间不少于1小时的学生人数.
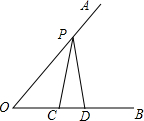 如图,∠AOB=60°,OP=12cm,OC=5cm,PC=PD,求OD的长.
如图,∠AOB=60°,OP=12cm,OC=5cm,PC=PD,求OD的长. 观察下面由分子是1的分数组成的排列,然后回答问题.
观察下面由分子是1的分数组成的排列,然后回答问题.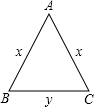 如图,等腰三角形ABC的周长为20cm,底边BC长为y(cm),腰AB长为x(cm)
如图,等腰三角形ABC的周长为20cm,底边BC长为y(cm),腰AB长为x(cm) 病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y(毫克)与时间x(小时)满足:前1小时内成正比例递增,1小时后按反比例函数图象衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y(毫克)与时间x(小时)满足:前1小时内成正比例递增,1小时后按反比例函数图象衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.