题目内容
 如图,已知△ABC中,若BC=6,△ABC的面积为12,四边形DEFG是△ABC的内接的正方形,则正方形DEFG的边长是
如图,已知△ABC中,若BC=6,△ABC的面积为12,四边形DEFG是△ABC的内接的正方形,则正方形DEFG的边长是考点:相似三角形的判定与性质,正方形的性质
专题:
分析:如图,作辅助线;证明DE=DG=MN(设为λ),得到AM=AN-λ;证明△ADG∽△ABC,列出比例式
=
,求出λ即可解决问题.
| 4-λ |
| 4 |
| λ |
| 6 |
解答: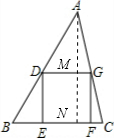 解:如图,过点A作AN⊥BC,交DG于点M;
解:如图,过点A作AN⊥BC,交DG于点M;
∵四边形DEFG是正方形,
∴DE=DG=MN(设为λ),则AM=AN-λ;
∵BC=6,△ABC的面积为12,
∴
×6AN=12,
∴AN=4,AM=4-λ;
∵DG∥BC,
∴△ADG∽△ABC,
∴
=
,
解得:λ=
.
故答案为
.
 解:如图,过点A作AN⊥BC,交DG于点M;
解:如图,过点A作AN⊥BC,交DG于点M;∵四边形DEFG是正方形,
∴DE=DG=MN(设为λ),则AM=AN-λ;
∵BC=6,△ABC的面积为12,
∴
| 1 |
| 2 |
∴AN=4,AM=4-λ;
∵DG∥BC,
∴△ADG∽△ABC,
∴
| 4-λ |
| 4 |
| λ |
| 6 |
解得:λ=
| 12 |
| 5 |
故答案为
| 12 |
| 5 |
点评:该题以正方形为载体,主要考查了相似三角形的判定及其性质的应用问题;解题的关键是灵活运用相似三角形的判定及其性质等来分析、判断、推理或解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
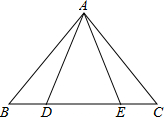 如图,等腰三角形ABC中,AB=AC,D、E都在BC上,要使△ABD≌△ACE,需要添加一个条件,某学习小组在讨论这个条件时给出了如下几种方案:
如图,等腰三角形ABC中,AB=AC,D、E都在BC上,要使△ABD≌△ACE,需要添加一个条件,某学习小组在讨论这个条件时给出了如下几种方案: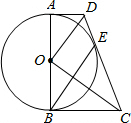 如图,在四边形ABCD中,AD∥BC,AD<BC,∠ABC=90°,以AB为直径作⊙O,恰与CD相切于点E,连接OD,OC,BE,
如图,在四边形ABCD中,AD∥BC,AD<BC,∠ABC=90°,以AB为直径作⊙O,恰与CD相切于点E,连接OD,OC,BE,