题目内容
 如图,直线y=-x+4与x轴、y轴分别交于点A,点B,点P的坐标为(-2,2),则S△PAB=
如图,直线y=-x+4与x轴、y轴分别交于点A,点B,点P的坐标为(-2,2),则S△PAB=考点:坐标与图形性质,三角形的面积
专题:
分析:作PC⊥x轴于C,如图,根据坐标轴上点的坐标特征求出A(4,0)、B(0,4),然后根据三角形面积公式和梯形的面积公式以及S△PAB=S梯形BOCP+S△ABO-S△APC进行计算.
解答:解: 作PC⊥x轴于C,如图,
作PC⊥x轴于C,如图,
当y=0时,-x+4=0,解得x=4,则A(4,0);
当x=0时,y=-x+4=4,则B(0,4),
所以S△PAB=S梯形BOCP+S△ABO-S△APC
=
×(2+4)×2+
×4×4-
×(4+2)×2
=8.
故答案为8.
 作PC⊥x轴于C,如图,
作PC⊥x轴于C,如图,当y=0时,-x+4=0,解得x=4,则A(4,0);
当x=0时,y=-x+4=4,则B(0,4),
所以S△PAB=S梯形BOCP+S△ABO-S△APC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=8.
故答案为8.
点评:本题考查了坐标与图形性质:利用点的坐标计算相应的线段长和判断线段与坐标轴的位置关系.若坐标系内的四边形是非规则四边形,通常用平行于坐标轴的辅助线用“割、补”法去解决问题.

练习册系列答案
相关题目
 如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,则正五边形的边长与正六边形的边长之比为( )
如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,则正五边形的边长与正六边形的边长之比为( )| A、6:5 | B、5:11 |
| C、5:6 | D、1:1 |
 如图,沪闵公路上A、B两地相距6km,C、D为两个小区,DA⊥AB,CB⊥AB,垂足分别为点A、B,已知DA长2km,CB长3km,现要在公路AB上建一个大卖场E,使得C、D两个小区到大卖场E的距离相等.
如图,沪闵公路上A、B两地相距6km,C、D为两个小区,DA⊥AB,CB⊥AB,垂足分别为点A、B,已知DA长2km,CB长3km,现要在公路AB上建一个大卖场E,使得C、D两个小区到大卖场E的距离相等. 已知:△ABC,用刻度尺量出△ABC的各边的长度,并取各边的中点,画出△ABC的三条中线,你发现了什么?
已知:△ABC,用刻度尺量出△ABC的各边的长度,并取各边的中点,画出△ABC的三条中线,你发现了什么?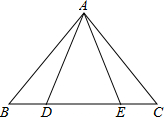 如图,等腰三角形ABC中,AB=AC,D、E都在BC上,要使△ABD≌△ACE,需要添加一个条件,某学习小组在讨论这个条件时给出了如下几种方案:
如图,等腰三角形ABC中,AB=AC,D、E都在BC上,要使△ABD≌△ACE,需要添加一个条件,某学习小组在讨论这个条件时给出了如下几种方案: