题目内容
如图，在四边形ABCE中，点D在对角线BE上，且| AB |
| AD |
| BC |
| DE |
| AC |
| AE |
考点：相似三角形的判定
专题：证明题
分析：根据三组对应边的比相等的两个三角形相似，由
=
=
得到△ABC∽△ADE，则∠BAC=∠DAE，所以∠BAD=∠CAE，由于
=
，根据比例性质得
=
，所以△ABD∽△ACE．
| AB |
| AD |
| BC |
| DE |
| AC |
| AE |
| AB |
| AD |
| AC |
| AE |
| AB |
| AC |
| AD |
| AE |
解答：证明：∵
=
=
，
∴△ABC∽△ADE，
∴∠BAC=∠DAE，
∴∠BAD=∠CAE，
而
=
，
∴
=
，
∴△ABD∽△ACE．
| AB |
| AD |
| BC |
| DE |
| AC |
| AE |
∴△ABC∽△ADE，
∴∠BAC=∠DAE，
∴∠BAD=∠CAE，
而
| AB |
| AD |
| AC |
| AE |
∴
| AB |
| AC |
| AD |
| AE |
∴△ABD∽△ACE．
点评：本题考查了相似三角形的判定：三组对应边的比相等的两个三角形相似；有两组角对应相等的两个三角形相似．
练习册系列答案
发散思维新课堂系列答案
相关题目
已知：△ABC，用刻度尺量出△ABC的各边的长度，并取各边的中点，画出△ABC的三条中线，你发现了什么？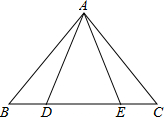
如图，等腰三角形ABC中，AB=AC，D、E都在BC上，要使△ABD≌△ACE，需要添加一个条件，某学习小组在讨论这个条件时给出了如下几种方案：