题目内容
5.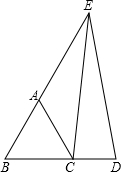 如图,△ABC为等边三角形,延长BC到D,又延长BA到E,使AE=BD,连接CE,DE,求证:△CDE为等腰三角形.
如图,△ABC为等边三角形,延长BC到D,又延长BA到E,使AE=BD,连接CE,DE,求证:△CDE为等腰三角形.
分析 延长BD至F,使DF=BC,连接EF,由AE=BD,三角形ABC为等边三角形,得到AB=BC=AC,且∠B=60°,利用等式的性质及等量代换得到BE=BF,进而得到三角形BEF为等边三角形,即∠F=60°,利用SAS得到三角形ECB和三角形DEF全等,利用全等三角形对应边相等即可得证.
解答 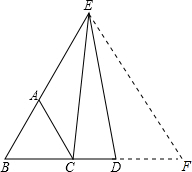 证明:延长BD至F,使DF=BC,连接EF,
证明:延长BD至F,使DF=BC,连接EF,
∵AE=BD,△ABC为等边三角形,
∴DF=BC=AB,即AE+AB=BD+DF,∠B=60°,
∴BE=BF,
∴△BEF为等边三角形,
∴∠F=60°,
在△ECB和△EDF中,
$\left\{\begin{array}{l}{BE=EF}\\{∠B=∠F=60°}\\{BC=DF}\end{array}\right.$
∴△ECB≌△EDF(SAS),
∴EC=ED,
即△CDE为等腰三角形.
点评 此题考查了全等三角形的判定与性质,以及等边三角形的判定与性质,熟练运用全等三角形的判定与性质进行推理是解本题的关键.

练习册系列答案
相关题目
14.已知单项式4x3ym与-3xn-1y3的和是单项式,则这两个单项式的和是( )
| A. | x2y3 | B. | x3y2 | C. | xn-1ym | D. | xn+2ym+2 |
15.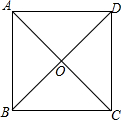 如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )
如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )
 如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )
如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )| A. | AO=BO=CO=DO,AC⊥BD | B. | AC=BC=CD=DA | ||
| C. | AO=CO,BO=DO,AC⊥BD | D. | AB=BC,CD⊥DA |
 已知:如图,△ABC是等边三角形,与BC平行的直线分别交AB和AC于点D,E,求证:△ADE是等边三角形.
已知:如图,△ABC是等边三角形,与BC平行的直线分别交AB和AC于点D,E,求证:△ADE是等边三角形. 如图,在△ABC中,∠ACB=90°,AC=BC=6,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示),那么,在上述旋转过程中:
如图,在△ABC中,∠ACB=90°,AC=BC=6,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示),那么,在上述旋转过程中: 已知直线m,n之间的距离是3,△ABC的顶点A在直线m上,边BC在直线n上,求△ABC的面积S和BC边的长x之间的关系式,并指出其中的变量和常量.
已知直线m,n之间的距离是3,△ABC的顶点A在直线m上,边BC在直线n上,求△ABC的面积S和BC边的长x之间的关系式,并指出其中的变量和常量. 如图:已知直线y1=-2x+3和直线y2=mx-1分别交y轴于点A、B,两直线交于点C(1,n).
如图:已知直线y1=-2x+3和直线y2=mx-1分别交y轴于点A、B,两直线交于点C(1,n).