��Ŀ����
9����֪�ڡ�ABC�У���BAC=90�㣬����C��ֱ��EF��AB��D��BC��һ�㣬����AD������D�ֱ���GD��AD��HD��BC����EF��AC�ڵ�G��H������AG��
��1������ACB=30��ʱ����ͼ1��ʾ��
����֤����GCD�ס�AHD��
�����ж�AD��DG֮���������ϵ����˵�����ɣ�
��2����tan��ACB=$\frac{4}{5}$ʱ����ͼ2��ʾ������ֱ��д��AD��DG֮���������ϵ��
���� ��1���ٸ���ƽ���ߵ����ʵõ���GCM=��BAC=90�㣬���ݴ�ֱ�Ķ���õ���ADM=90�㣬������á�GCA=��ADM���Ƴ���DAH=��CGD���������������ε��ж��������ɵõ����ۣ��ڸ������������ε����ʵõ�$\frac{AD}{DG}=\frac{DH}{CD}$���������Ǻ����Ķ��弴�ɵõ����ۣ�
��2���������������ε����ʵõ�$\frac{AD}{DG}=\frac{DH}{CD}$������tan��ACB=$\frac{4}{5}$�����ɵõ����ۣ�
���  ��1����֤�����ߡ�BAC=90�㣬EF��AB��
��1����֤�����ߡ�BAC=90�㣬EF��AB��
���GCM=��BAC=90�㣬
��GD��AD��
���ADM=90�㣬
���GCA=��ADM��
�ߡ�AMD=��GMC��
���DAH=��CGD��
�ߡ�ADH=��CDG=90��-��HDG
���GCD�ס�AHD��
�ڽ⣺�ɢ�֪����GCD�ס�AHD��
��$\frac{AD}{DG}=\frac{DH}{CD}$��
��Rt��DHC��
�ߡ�ACB=30�㣬
$\frac{DH}{CD}$=tan30��=$\frac{\sqrt{3}}{3}$��
��$\frac{AD}{DG}=\frac{DH}{CD}$=$\frac{\sqrt{3}}{3}$��
��2��5AD=4DG��
�⣺�ɢ�֪��GCD�ס�AHD��
��Rt��DHC��
��tan��ACB=$\frac{4}{5}$��
��$\frac{AD}{DG}=\frac{DH}{CD}$=$\frac{4}{5}$��
���� ���⿼�������������ε��ж������ʣ�ƽ���ߵ����ʣ����Ǻ����Ķ��壬�����������������ε��ж��������ǽ���Ĺؼ���

��x2-4x+m=x2+��n+3��x+3n��
��$\left\{\begin{array}{l}{n+3=-4}\\{m=3n}\end{array}\right.$��ã�n=-7��m=-21��
����һ����ʽΪx-7��m��ֵΪ-21��
���Ƶأ���������ʽ2x2+3x-k��һ����ʽ��2x-5����������һ����ʽ�Լ�k��ֵΪ��������
| A�� | x-1��5 | B�� | x+4��20 | C�� | x$+\frac{3}{2}$��$\frac{15}{2}$ | D�� | x+4��-4 |
| A�� | ����������ɵ�ͼ�ν����� | B�� | ��AB=BC�����B��AC���е� | ||
| C�� | ����֮��ֱ����� | D�� | ����ȷ��һ��ֱ�� |
 ��ͼ��AB��CD����AO=CO����֤��AB=CD��
��ͼ��AB��CD����AO=CO����֤��AB=CD�� �����Ŵ�С��ͬ��������ֽƬ�ڷ���ͼ��ʾλ�ã��ǡ�1�Ķ���Ϊ57�㣮
�����Ŵ�С��ͬ��������ֽƬ�ڷ���ͼ��ʾλ�ã��ǡ�1�Ķ���Ϊ57�㣮 ��ͼ��A��B��C��D��ֱ��l�ϵ��ĸ��㣬M��N�ֱ���AB��CD���е㣮
��ͼ��A��B��C��D��ֱ��l�ϵ��ĸ��㣬M��N�ֱ���AB��CD���е㣮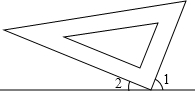 ���ǰ��ֱ�Ƕ�����ֱ��l�ϣ�����1=40��15�䣬���2�Ķ�����49��45�䣮
���ǰ��ֱ�Ƕ�����ֱ��l�ϣ�����1=40��15�䣬���2�Ķ�����49��45�䣮 ��ͼ����������dz��е�һ�ֱ�����ͨ���ߣ�����ABC�������г˳����������y��Ԫ�����г����x��km��֮��ĺ�����ϵͼ��
��ͼ����������dz��е�һ�ֱ�����ͨ���ߣ�����ABC�������г˳����������y��Ԫ�����г����x��km��֮��ĺ�����ϵͼ��