题目内容
9.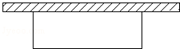 利用一面墙(墙的长度为20m),另三边用48m长的篱笆围成一个矩形场地.
利用一面墙(墙的长度为20m),另三边用48m长的篱笆围成一个矩形场地.(1)若场地的面积为160m2,求矩形场地的长和宽;
(2)场地的面积能否达到300m2?若能,请求出矩形场地的长和宽;若不能,请说明理由.
分析 (1)设该矩形的长为x(0<x≤20),根据矩形的面积列出方程并解答;
(2)假设场地的面积能否达到300m2.据此求得相应的长,看该数值是否符合题意即可.
解答 解:(1)设该矩形的长为x(0<x≤20),根据题意得:
$\frac{1}{2}$(48-x)x=160,
解得x=40(舍去)或x=8,
则$\frac{1}{2}$(48-x)=$\frac{1}{2}$(48-8)=10.
答:矩形场地的长是8cm,宽是10cm;
(2)设长为ym,根据题意得:
$\frac{1}{2}$(48-x)x=300,
整理得:y2-48y+600=0,
∵b2-4ac=2304-2400=-96<0,
∴此方程无实数根.
答:场地的面积不能达到300m2.
点评 本题考查了矩形的面积公式的运用,一元二次方程的解法的运用,根的判别式的运用,根据题意结合矩形面积得出等式方程是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.设n为正整数,若64n-7n能被57整除,则82n+1+7n+2能被下列哪个数整除( )
| A. | 55 | B. | 56 | C. | 57 | D. | 58 |
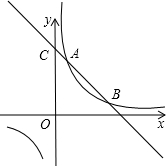 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的交于点A(1,4)和点B,与y轴交于点C(0,5).求:
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的交于点A(1,4)和点B,与y轴交于点C(0,5).求:
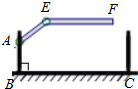 某地下车库出口处安装了“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图所示的位置,其中AB⊥BC,EF∥BC,∠AEF=135°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为(栏杆宽度忽略不计.参考数据:$\sqrt{2}$≈1.4)( )
某地下车库出口处安装了“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图所示的位置,其中AB⊥BC,EF∥BC,∠AEF=135°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为(栏杆宽度忽略不计.参考数据:$\sqrt{2}$≈1.4)( )


