题目内容
19.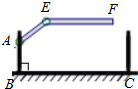 某地下车库出口处安装了“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图所示的位置,其中AB⊥BC,EF∥BC,∠AEF=135°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为(栏杆宽度忽略不计.参考数据:$\sqrt{2}$≈1.4)( )
某地下车库出口处安装了“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图所示的位置,其中AB⊥BC,EF∥BC,∠AEF=135°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为(栏杆宽度忽略不计.参考数据:$\sqrt{2}$≈1.4)( )| A. |  | B. |  | C. |  | D. |  |
分析 过点A作BC的平行线AG,过点E作EH⊥AG于H,则∠BAG=90°,∠EHA=90°.先求出∠AEH=45°,则∠EAH=45°,然后在△EAH中,利用正弦函数的定义得出EH=AE•sin∠EAH,则栏杆EF段距离地面的高度为:AB+EH,代入数值计算即可.
解答 解:如图,过点A作BC的平行线AG,过点E作EH⊥AG于H,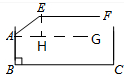
则∠EHG=∠HEF=90°,
∵∠AEF=135°,
∴∠AEH=∠AEF-∠HEF=45°,
∠EAH=45°,
在△EAH中,∠EHA=90°,∠EAH=45°,AE=1.3米,
∴EH=AE•sin∠EAH≈1.3×0.7=0.91(米),
∵AB=1.3米,
∴AB+EH≈1.3+0.91=1.92≈2.2米.
故选B.
点评 本题考查了解直角三角形在实际中的应用,关键是通过作辅助线,构造直角三角形,把实际问题转化为数学问题加以计算.

练习册系列答案
相关题目
10.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出20件.设每件商品降价x元后,每星期售出商品的总销售额为y元,则y与x的关系式为( )
| A. | y=60(300+20x) | B. | y=(60-x)(300+20x) | C. | y=300(60-20x) | D. | y=(60-x)(300-20x) |
14.若△ABC∽△DEF,相似比为1:3,则△ABC与△DEF的面积比为( )
| A. | 1:9 | B. | 1:3 | C. | 1:2 | D. | 1:$\sqrt{3}$ |
11.若$\frac{x}{y}$=$\frac{4}{5}$,则$\frac{2x-y}{x+y}$的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{3}{2}$ |
8.点P(2,-3)关于x轴对称的点是( )
| A. | (-2,3) | B. | (2,3) | C. | (-2,-3) | D. | (2,-3) |
 利用一面墙(墙的长度为20m),另三边用48m长的篱笆围成一个矩形场地.
利用一面墙(墙的长度为20m),另三边用48m长的篱笆围成一个矩形场地. 已知:如图,D是BC上一点,△ABC∽△ADE,求证:∠1=∠2=∠3.
已知:如图,D是BC上一点,△ABC∽△ADE,求证:∠1=∠2=∠3.