题目内容
17.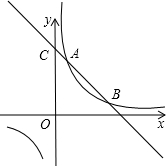 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的交于点A(1,4)和点B,与y轴交于点C(0,5).求:
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的交于点A(1,4)和点B,与y轴交于点C(0,5).求:(1)求点B的坐标;
(2)点P是x轴上的一动点,当PA+PB最小时,求点P的坐标.
分析 (1)把A坐标代入y=$\frac{k}{x}$求得k,把A、C的坐标代入y=ax+b求得a、b,然后两解析式联立方程即可求得B的坐标;
(2)作B的对称点B′,连接AB′,交x轴于P,此时PA+PB=AB′最小,根据B的坐标求得B′的坐标,然后根据待定系数法求得直线AB′的解析式,进而求得与x轴的交点即可.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$经过点A(1,4),
∴k=1×4=4,
∴反比例函数为y=$\frac{4}{x}$,
∵一次函数y=ax+b经过A(1,4),C(0,5),
∴$\left\{\begin{array}{l}{a+b=4}\\{b=5}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=5}\end{array}\right.$,
∴一次函数为y=-x+5,
解$\left\{\begin{array}{l}{y=\frac{4}{x}}\\{y=-x+5}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$,
∴B(4,1);
(2)作B的对称点B′,连接AB′,交x轴于P,此时PA+PB=AB′最小,
∵B(4,1),
∴B′(4,-1),
设直线AB′的解析式为y=mx+n,
∴$\left\{\begin{array}{l}{m+n=4}\\{4m+n=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-\frac{5}{3}}\\{n=\frac{17}{3}}\end{array}\right.$,
∴直线AB′的解析式为y=-$\frac{5}{3}$x+$\frac{17}{3}$,
令y=0,得-$\frac{5}{3}$x+$\frac{17}{3}$=0,解得x=$\frac{17}{5}$,
∴点P的坐标为($\frac{17}{5}$,0).
点评 本题主要考查反比例函数和一次函数的交点及待定系数法求函数解析式、轴对称-最短路线问题,掌握图象的交点的坐标满足两个函数解析式是解题的关键.

| A. | 对角线互相平分 | B. | 对角相等 | C. | 对角线互相垂直 | D. | 4个内角都相等 |
| A. | 不相交的两条直线叫做平行线 | |
| B. | 相等的角是对顶角 | |
| C. | 过直线外一点有且只有一条直线与已知直线平行 | |
| D. | 过一点有且只有一条直线与已知直线垂直 |
①-3.14既是负数,分数,也是有理数;
②0既不是正数,也不是负数,但是整数;
③0是正数和负数的分界;
④-200既是负数,也是整数,但不是有理数.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 平均数是80 | B. | 极差是15 | C. | 中位数是75 | D. | 方差是25 |
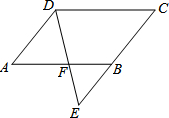 已知:如图,?ABCD中,E是CB延长线上一点,DE交AB于F.求证:AD•CD=AF•CE.
已知:如图,?ABCD中,E是CB延长线上一点,DE交AB于F.求证:AD•CD=AF•CE. 利用一面墙(墙的长度为20m),另三边用48m长的篱笆围成一个矩形场地.
利用一面墙(墙的长度为20m),另三边用48m长的篱笆围成一个矩形场地. 已知:如图,D是BC上一点,△ABC∽△ADE,求证:∠1=∠2=∠3.
已知:如图,D是BC上一点,△ABC∽△ADE,求证:∠1=∠2=∠3.