题目内容
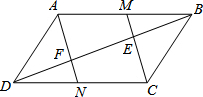 已知,M、N分别是平行四边形ABCD的边AB、CD的中点,CM、AN分别交BD于E、F.求证:BE=EF=FD.
已知,M、N分别是平行四边形ABCD的边AB、CD的中点,CM、AN分别交BD于E、F.求证:BE=EF=FD.考点:平行四边形的性质,三角形中位线定理
专题:证明题
分析:已知平行四边形ABCD,可证△AFB∽△NFD.,根据三角形相似的性质可求出线段的比,然后进一步解答.
解答: 证明:在平行四边形ABCD中,
证明:在平行四边形ABCD中,
∴AD∥BC,
∴△AFB∽△NFD.
∴DF:BF=DN:AB,
∵N为DC的中点,
∴DF:BF=DN:AB=1:2,
即DF=
BD,
同理BE=
BD,
则EF=BD-DF-BE=BD-
BD-
BD=
BD,
∴DF=EF=BE.
 证明:在平行四边形ABCD中,
证明:在平行四边形ABCD中,∴AD∥BC,
∴△AFB∽△NFD.
∴DF:BF=DN:AB,
∵N为DC的中点,
∴DF:BF=DN:AB=1:2,
即DF=
| 1 |
| 3 |
同理BE=
| 1 |
| 3 |
则EF=BD-DF-BE=BD-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴DF=EF=BE.
点评:此题主要考查了平行四边形的性质和相似三角形的判定与性质,解答此题要根据平行四边形的性质得出AB=CD,然后根据三角形相似求出相似比,然后进行线段的加减运算.

练习册系列答案
相关题目
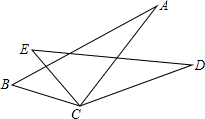 如图,从下列:①BC=EC,②AC=DC,③AB=DE,④∠ACD=∠BCE中任取三个为条件,余下的一个为结论,则最多可以构成正确说法的个数是( )
如图,从下列:①BC=EC,②AC=DC,③AB=DE,④∠ACD=∠BCE中任取三个为条件,余下的一个为结论,则最多可以构成正确说法的个数是( )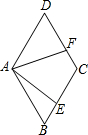 如图,在菱形ABCD中,AB=3,∠ABC=60°,点E、F分别在直线BC、CD上,CF=1,若∠EAF=60°,求△CEF的面积.
如图,在菱形ABCD中,AB=3,∠ABC=60°,点E、F分别在直线BC、CD上,CF=1,若∠EAF=60°,求△CEF的面积. 在平行四边形ABCD中,点E为AD的中点,连接CE,点M、N为CE上两点,且BM∥DN.连接DM并延长交AB于F,若BF=2AF,求
在平行四边形ABCD中,点E为AD的中点,连接CE,点M、N为CE上两点,且BM∥DN.连接DM并延长交AB于F,若BF=2AF,求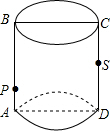 如图所示,圆柱的轴截面ABCD是边长为4的正方形,动点P的初始位置在AB上,AP=1,点P由此出发,沿着圆柱的侧面移动到CD的中点S,点P与点S之间的最短距离是
如图所示,圆柱的轴截面ABCD是边长为4的正方形,动点P的初始位置在AB上,AP=1,点P由此出发,沿着圆柱的侧面移动到CD的中点S,点P与点S之间的最短距离是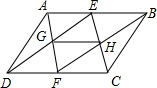 如图所示,在?ABCD中,点E、F分别是AB、CD的中点,连接AF、DE、BF、CE,AF与DE交于点G,BF与CE交于点H,连接GH,求证:GH∥DC且GH=
如图所示,在?ABCD中,点E、F分别是AB、CD的中点,连接AF、DE、BF、CE,AF与DE交于点G,BF与CE交于点H,连接GH,求证:GH∥DC且GH=