题目内容
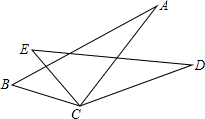 如图,从下列:①BC=EC,②AC=DC,③AB=DE,④∠ACD=∠BCE中任取三个为条件,余下的一个为结论,则最多可以构成正确说法的个数是( )
如图,从下列:①BC=EC,②AC=DC,③AB=DE,④∠ACD=∠BCE中任取三个为条件,余下的一个为结论,则最多可以构成正确说法的个数是( )| A、1 | B、2 | C、3 | D、4 |
考点:全等三角形的判定与性质
专题:
分析:取3个作为条件,一一证明△ACB≌△DCE即可,根据组合的个数即可解题.
解答:解:(1)①②③为条件④为结论,
在△ACB和△DCE中,
,
∴△ACB≌△DCE(SSS),
∴∠DCE=∠ACB,
∴∠ACD=∠BCE;
(2)①②④为条件③为结论,
∵∠ACD=∠BCE,
∴∠DCE=∠ACB,
在△ACB和△DCE中,
,
∴△ACB≌△DCE(SAS),
∴AB=DE,
其余均不可证明,
故选B.
在△ACB和△DCE中,
|
∴△ACB≌△DCE(SSS),
∴∠DCE=∠ACB,
∴∠ACD=∠BCE;
(2)①②④为条件③为结论,
∵∠ACD=∠BCE,
∴∠DCE=∠ACB,
在△ACB和△DCE中,
|
∴△ACB≌△DCE(SAS),
∴AB=DE,
其余均不可证明,
故选B.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角、对应边比例相等的性质,本题中根据条件证明△ACB≌△DCE是解题的关键.

练习册系列答案
相关题目
 如图,AB是⊙0的直径,点C在⊙0上,∠B=65°,则∠A=( )
如图,AB是⊙0的直径,点C在⊙0上,∠B=65°,则∠A=( )| A、20° | B、25° |
| C、30° | D、35° |
 如图,矩形ABCD沿AE折叠,使D点落在BC边上点F处,如果∠BAF=60°,则∠EAF等于( )
如图,矩形ABCD沿AE折叠,使D点落在BC边上点F处,如果∠BAF=60°,则∠EAF等于( )| A、15° | B、30° |
| C、45° | D、60° |
在下面的图形中是正方体的展开图的为( )
A、 |
B、 |
C、 |
D、 |
在1:5000的地图上,A、B两地的图上距离为3cm,则A、B两地间实际距离为( )
| A、15m | B、150m |
| C、1500m | D、15000m |
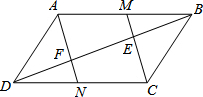 已知,M、N分别是平行四边形ABCD的边AB、CD的中点,CM、AN分别交BD于E、F.求证:BE=EF=FD.
已知,M、N分别是平行四边形ABCD的边AB、CD的中点,CM、AN分别交BD于E、F.求证:BE=EF=FD.