题目内容
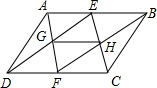 如图所示,在?ABCD中,点E、F分别是AB、CD的中点,连接AF、DE、BF、CE,AF与DE交于点G,BF与CE交于点H,连接GH,求证:GH∥DC且GH=
如图所示,在?ABCD中,点E、F分别是AB、CD的中点,连接AF、DE、BF、CE,AF与DE交于点G,BF与CE交于点H,连接GH,求证:GH∥DC且GH=| 1 |
| 2 |
考点:平行四边形的性质,全等三角形的判定与性质,三角形中位线定理
专题:证明题
分析:由在?ABCD中,点E、F分别是AB、CD的中点,易证得△AEG≌△FDG(AAS),可得EG=DG,同理可证得EH=CH,即可得GH是△ECD的中位线,继而证得结论.
解答:证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠GAE=∠GFD,
∵点E、F分别是AB、CD的中点,
∴AE=DF,
在△AEG和△FDG中,
,
∴△AEG≌△FDG(AAS),
∴EG=DG,
同理:EH=CH,
∴GH∥DC且GH=
DC.
∴AB∥CD,AB=CD,
∴∠GAE=∠GFD,
∵点E、F分别是AB、CD的中点,
∴AE=DF,
在△AEG和△FDG中,
|
∴△AEG≌△FDG(AAS),
∴EG=DG,
同理:EH=CH,
∴GH∥DC且GH=
| 1 |
| 2 |
点评:此题考查了平行四边形的性质、三角形中位线的性质以及全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
下列方程中是一元二次方程的是( )
| A、ax2+bx+c=0 | ||
| B、x2=x(x+2)+3 | ||
| C、x2-1=0 | ||
D、x2+
|
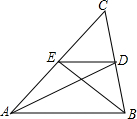 如图,△ABC中,E、D分别是AC、BC的中点,则S△CDE:SABDE=( )
如图,△ABC中,E、D分别是AC、BC的中点,则S△CDE:SABDE=( )| A、1:4 | B、2:3 |
| C、1:3 | D、1:2 |
下列各组中,属于同类项的是( )
A、
| ||
| B、7x2y与x2y | ||
| C、2mnp与2mn | ||
| D、0.5pq与-pqn |
比-1小1的数是( )
| A、-2 | B、0 | C、1 | D、-1 |
下列各组数中,互为相反数的是( )
A、
| ||
B、-2和-
| ||
| C、-2和|-2| | ||
D、-2和
|
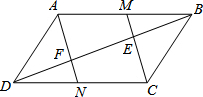 已知,M、N分别是平行四边形ABCD的边AB、CD的中点,CM、AN分别交BD于E、F.求证:BE=EF=FD.
已知,M、N分别是平行四边形ABCD的边AB、CD的中点,CM、AN分别交BD于E、F.求证:BE=EF=FD.