题目内容
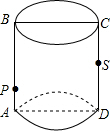 如图所示,圆柱的轴截面ABCD是边长为4的正方形,动点P的初始位置在AB上,AP=1,点P由此出发,沿着圆柱的侧面移动到CD的中点S,点P与点S之间的最短距离是
如图所示,圆柱的轴截面ABCD是边长为4的正方形,动点P的初始位置在AB上,AP=1,点P由此出发,沿着圆柱的侧面移动到CD的中点S,点P与点S之间的最短距离是考点:平面展开-最短路径问题
专题:
分析:先求出底边半径的长,再把圆柱的侧面展开,根据勾股定理求出PS的长即可.
解答: 解:如图所示,
解:如图所示,
∵圆柱的轴截面ABCD是边长为4的正方形,
∴AD=2π,
∵S是CD的中点,
∴SD=2,
∴PS=
=
.
故答案为:
.
 解:如图所示,
解:如图所示,∵圆柱的轴截面ABCD是边长为4的正方形,
∴AD=2π,
∵S是CD的中点,
∴SD=2,
∴PS=
| (2π)2+12 |
| 1+4π2 |
故答案为:
| 1+4π2 |
点评:本题考查的是平面展开-最短路径问题,根据题意画出圆柱的侧面展开图,根据勾股定理求解即可.

练习册系列答案
相关题目
绝对值小于4.5的整数有( )
| A、10个 | B、9个 | C、8个 | D、7个 |
下列方程中是一元二次方程的是( )
| A、ax2+bx+c=0 | ||
| B、x2=x(x+2)+3 | ||
| C、x2-1=0 | ||
D、x2+
|
比-1小1的数是( )
| A、-2 | B、0 | C、1 | D、-1 |
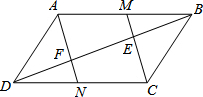 已知,M、N分别是平行四边形ABCD的边AB、CD的中点,CM、AN分别交BD于E、F.求证:BE=EF=FD.
已知,M、N分别是平行四边形ABCD的边AB、CD的中点,CM、AN分别交BD于E、F.求证:BE=EF=FD.