题目内容
9.化简与求值:(1)当5m-3n=-4时,求代数式2(m-n)+4(2m-n)+2的值;
(2)已知A=a2+4a-8,B=-$\frac{1}{2}$a2-3a+4,当a=-$\frac{3}{2}$时,求A-2(A-B)+3的值.
(3)已知多项式(mx2+nxy-3x+y-1)-(3x2-mxy-3x-1)的差与x的取值无关,求(-1)2008+m+n[m-n+(-n)m]的值.
分析 (1)原式去括号整理后,将已知等式代入计算即可求出值;
(2)把A与B代入原式计算得到最简结果,再将a的值代入计算即可求出值;
(3)多项式去括号整理后,根据结果与x的取值无关求出m与n的值,代入原式计算即可得到结果.
解答 解:(1)原式=2m-2n+8m-4n+2=10m-6n+2=2(5m-3n)+2,
当5m-3n=-4时,原式=-8+2=-6;
(2)∵A=a2+4a-8,B=-$\frac{1}{2}$a2-3a+4,
∴原式=A-2A+2B+3=-A+2B+3=-a2-4a+8-a2-6a+8+3=-2a2-10a+19,
当a=-$\frac{3}{2}$时,原式=-$\frac{9}{2}$+15+19=29$\frac{1}{2}$;
(3)原式=(m-3)x2+(m+n)xy+y,
结果与x的取值无关,得到m-3=0,且m+n=0,
解得:m=3,n=-3,
则原式=33.
点评 此题考查了整式的加减-化简求值,以及乘方的意义,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.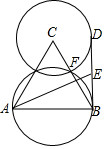 如图,已知等边△ABC的边长为4,以AB为直径的圆交BC于点F,以C为圆心,CF的长为半径作圆,D是⊙C上一动点,E为BD的中点,当AE最大时,BD的长为( )
如图,已知等边△ABC的边长为4,以AB为直径的圆交BC于点F,以C为圆心,CF的长为半径作圆,D是⊙C上一动点,E为BD的中点,当AE最大时,BD的长为( )
 如图,已知等边△ABC的边长为4,以AB为直径的圆交BC于点F,以C为圆心,CF的长为半径作圆,D是⊙C上一动点,E为BD的中点,当AE最大时,BD的长为( )
如图,已知等边△ABC的边长为4,以AB为直径的圆交BC于点F,以C为圆心,CF的长为半径作圆,D是⊙C上一动点,E为BD的中点,当AE最大时,BD的长为( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{3}$+1 | D. | 6 |
4.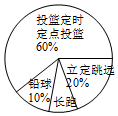 某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练后都进行了测训练后篮球定点投篮测试进行球赛进球统计表
某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练后都进行了测训练后篮球定点投篮测试进行球赛进球统计表
请你根据图表中信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为多少个?
(2)选择长跑训练的人数占全班人数的百分比是10%,该班共有同学40人;
(3)根据测试资料,参加蓝球定时定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
 某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练后都进行了测训练后篮球定点投篮测试进行球赛进球统计表
某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练后都进行了测训练后篮球定点投篮测试进行球赛进球统计表| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
(1)训练后篮球定时定点投篮人均进球数为多少个?
(2)选择长跑训练的人数占全班人数的百分比是10%,该班共有同学40人;
(3)根据测试资料,参加蓝球定时定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
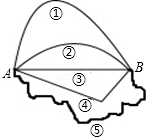 如图,从A地到B地共有五条路,人们常常选择第③条,请用几何知识解释原因两点之间,线段最短.
如图,从A地到B地共有五条路,人们常常选择第③条,请用几何知识解释原因两点之间,线段最短.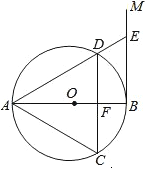 如图,AB是⊙O的直径,过点B作BM⊥AB,弦CD∥BM,交AB于点F,且DA=DC,连接AC,AD,延长AD交BM于点E.
如图,AB是⊙O的直径,过点B作BM⊥AB,弦CD∥BM,交AB于点F,且DA=DC,连接AC,AD,延长AD交BM于点E.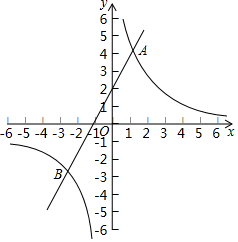 如图,直线y=2x+n与双曲线y=$\frac{m}{x}$(m≠0)交于A,B两点,且点A的坐标为(1,4).
如图,直线y=2x+n与双曲线y=$\frac{m}{x}$(m≠0)交于A,B两点,且点A的坐标为(1,4).