题目内容
14.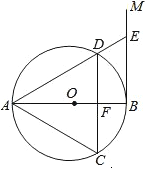 如图,AB是⊙O的直径,过点B作BM⊥AB,弦CD∥BM,交AB于点F,且DA=DC,连接AC,AD,延长AD交BM于点E.
如图,AB是⊙O的直径,过点B作BM⊥AB,弦CD∥BM,交AB于点F,且DA=DC,连接AC,AD,延长AD交BM于点E.(1)求证:△ACD是等边三角形;
(2)若AC=$\sqrt{3}$,求DE的长.
分析 (1)由BM⊥AB,CD∥BM,得到CD⊥AB,而AB是⊙O的直径,根据垂径定理得到$\widehat{AD}$=$\widehat{AC}$,于是得到AD=AC,然后根据已知DA=DC,得出AD=AC=CD,即可证明△ACD是等边三角形;
(2)过O作ON⊥AC于N,由垂径定理得到AN=$\frac{1}{2}$AC=$\frac{\sqrt{3}}{2}$,由(1)知,△ACD是等边三角形,根据等边三角形的性质得到∠CAB=30°,于是得到结论.
解答 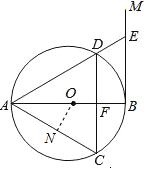 (1)证明:∵BM⊥AB,CD∥BM,
(1)证明:∵BM⊥AB,CD∥BM,
∴AB⊥CD,
∵AB是⊙O的直径,
∴$\widehat{AD}$=$\widehat{AC}$,
∴AD=AC,
∵DA=DC,
∴AD=AC=CD,
∴△ACD是等边三角形;
(2)解:过O作ON⊥AC于N,
则AN=$\frac{1}{2}$AC=$\frac{\sqrt{3}}{2}$,
由(1)知,△ACD是等边三角形,
∴∠DAC=60°.
∵AD=AC,CD⊥AB,
∴∠CAB=30°,
∴AO=$\frac{AN}{\frac{\sqrt{3}}{2}}$=1,
∴⊙O的半径为1.
点评 本题考查的是圆的切线的性质、等边三角形的判定、直角三角形的性质,掌握圆的切线垂直于经过切点的半径是解题的关键.

练习册系列答案
相关题目
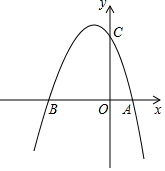 如图所示,抛物线与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C(0,3).
如图所示,抛物线与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C(0,3). 如图,用尺规作图在五边形ABCDE的边BC上找一点P,使∠APB=60°.(保留作图痕迹,不写作法)
如图,用尺规作图在五边形ABCDE的边BC上找一点P,使∠APB=60°.(保留作图痕迹,不写作法)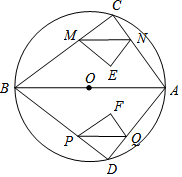 如图,⊙O是△ABC的外接圆,且AB是⊙O的直径,BC=8,AB=10,动点M在线段BC上从点C向点B运动.MN∥AB交AC于点N,四边形CMEN关于MN对称,△ABC与△ABD及四边形CMEN与四边形DPFQ都关于直线AB对称.
如图,⊙O是△ABC的外接圆,且AB是⊙O的直径,BC=8,AB=10,动点M在线段BC上从点C向点B运动.MN∥AB交AC于点N,四边形CMEN关于MN对称,△ABC与△ABD及四边形CMEN与四边形DPFQ都关于直线AB对称.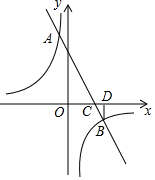 如图,已知一次函数y1=k1x+6与反比例函数y2=$\frac{{k}_{2}}{x}$相交于A、B,与x轴交于点C,过点B作BD⊥x轴于点D,已知sin∠DBC=$\frac{\sqrt{5}}{5}$,OC:CD=3:1.
如图,已知一次函数y1=k1x+6与反比例函数y2=$\frac{{k}_{2}}{x}$相交于A、B,与x轴交于点C,过点B作BD⊥x轴于点D,已知sin∠DBC=$\frac{\sqrt{5}}{5}$,OC:CD=3:1.