题目内容
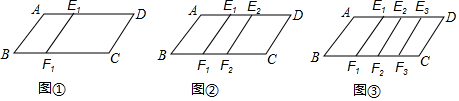
7.(1)如图①,四边形ABCD中,AB∥E1F1∥CD,AD∥BC,则图中共有3个平行四边形;(2)如图②,四边形ABCD中,AB∥E1F1∥E2F2∥CD,AD∥BC,则图中共有6个平行四边形;
(3)如图③,四边形ABCD中,AB∥E1F1∥E2F2∥E3F3∥CD,AD∥BC,则图中共有10个平行四边形.
探索:以此类推,一般地,若平行四边形ABCD中,E1,E2,E3,…,En都是AD上的点,F1,F2,F3,…,Fn都是BC上的点,且AB∥E1F1∥E2F2∥E3F3∥…∥EnFn,则图中共有$\frac{1}{2}$(n+1)(n-2)个平行四边形.
分析 (1)根据平行四边形的判定定理即可得到结论;
(2)根据平行四边形的判定定理即可得到结论;
(3)由(1)、(2)的结论即可得到结论.
解答 解:(1)∵AB∥E1F1∥CD,AD∥BC,
∴四边形ABCD,四边形ABE1F1,四边形CDE1F1是平行四边形,
∴图中共有3个平行四边形,
故答案为:3;
(2)∵AB∥E1F1∥E2F2∥CD,AD∥BC,
∴四边形ABCD,四边形ABE1F1,四边形E1F1E2F2,四边形CDE2F2,四边形ABE2F2,四边形CDE1F1是平行四边形,
∴图中共有6个平行四边形,
故答案为:6;
(3)由(1)、(2)知,∵AB∥E1F1∥E2F2∥E3F3∥CD,AD∥BC,则图中共有10个平行四边形,
∵AB∥E1F1∥E2F2∥E3F3∥…∥EnFn,则图中共有$\frac{1}{2}$(n+1)(n-2)个平行四边形.
故答案为:10,$\frac{1}{2}$(n+1)(n-2).
点评 本题考查了平行四边形的判定定理,熟练掌握平行四边形的判定定理是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
17.y关于x的一次函数y=2x+m2+1的图象不可能经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
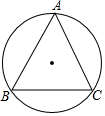 如图,△ABC中,BC=5,sinA=$\frac{3}{5}$
如图,△ABC中,BC=5,sinA=$\frac{3}{5}$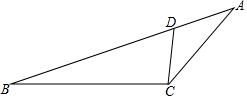 如图,点D在△ABC的AB边上,且∠ACD=∠A.
如图,点D在△ABC的AB边上,且∠ACD=∠A. 如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为8.
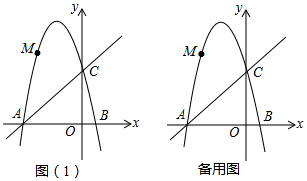
如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为8.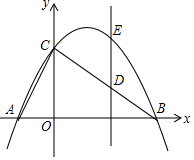 如图,Rt△ABC的三个顶点均落在平面直角坐标系的坐标轴上,OA=1,OB=4OA,∠ACB=90°,抛物线y=ax2+bx+c(a≠0)过A,B,C三点.
如图,Rt△ABC的三个顶点均落在平面直角坐标系的坐标轴上,OA=1,OB=4OA,∠ACB=90°,抛物线y=ax2+bx+c(a≠0)过A,B,C三点.