题目内容
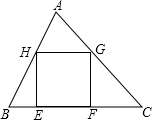如图，在△ABC中，正方形EFGH的两个顶点E、F在BC上，另两个顶点G、H分别在AC、AB上，BC=15cm，BC边上的高是10cm，求正方形的面积．考点：相似三角形的判定与性质,正方形的性质
专题：
分析：如图，作辅助线；证明△AHG∽△ABC，进而求出HG的长，即可解决问题．
解答：
解：如图，作AD⊥BC，交GH于点M；
∵四边形EFGH是正方形，
∴EH=MD=HG（设为λ），
则AM=10-λ；AM⊥GH；
∵GH∥BC，
∴△AHG∽△ABC，
∴
=
，即
=
，
解得：λ=6，
∴该正方形的面积=36（cm2）．
解：如图，作AD⊥BC，交GH于点M；∵四边形EFGH是正方形，
∴EH=MD=HG（设为λ），
则AM=10-λ；AM⊥GH；
∵GH∥BC，
∴△AHG∽△ABC，
∴
| GH |
| BC |
| AM |
| AD |
| λ |
| 15 |
| 10-λ |
| 10 |
解得：λ=6，
∴该正方形的面积=36（cm2）．
点评：该题主要考查了正方形的性质、相似三角形的判定及其性质等几何知识点的应用问题；作辅助线，灵活运用有关定理来分析、判断、推理或解答是解题的关键．
练习册系列答案
相关题目
已知一个四棱锥的正视图和俯视图如图所示，其中a+b=10，则该四棱锥体积的最大值为（ ）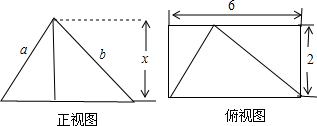
A、8
| ||
B、24
| ||
| C、16 | ||
| D、48 |
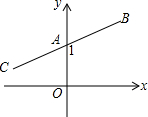如图，点A，点B的坐标分别是（0，1），（a，b），将线段AB绕A旋转180°后得到线段AC，则点C的坐标为（ ）| A、（-a，-b+1） |
| B、（-a，-b-1） |
| C、（-a，-b+2） |
| D、（-a，-b-2） |
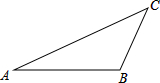（1）已知：如图，△ABC，求作：点P，使得PC∥AB，且△ABP是以AB为底的等腰三角形（要求：尺规左图，保留作图痕迹）
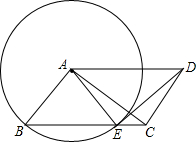如图，在?ABCD中，AB⊥AC，以点A为圆心，AB为半径的圆交BC于点E．
如图，这是一个由小立方体搭成的几何体的俯视图，小正方形中的数字表示位置的小立方体的个数．请画出它的主视图与左视图．