题目内容
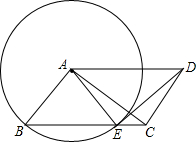 如图,在?ABCD中,AB⊥AC,以点A为圆心,AB为半径的圆交BC于点E.
如图,在?ABCD中,AB⊥AC,以点A为圆心,AB为半径的圆交BC于点E.(1)求证:DE为⊙O的切线;
(2)如果BE=4,CE=2,求DE的值.
考点:切线的判定,平行四边形的性质
专题:证明题
分析:(1)根据平行四边形的性质得AB=CD,BC=AD,AB∥CD,∠B=∠ADC,由AB⊥AC得到AC⊥CD,由AD∥BC得到∠AEB=∠DAE,而AB=AE,所以∠B=∠AEB,AE=DC,∠DAE=∠ADC,于是可证明△AED≌△DCA,得到∠AED=∠DCA=90°,则可根据切线的判定定理得到DE为⊙O的切线;
(2)作AH⊥BE,如图,根据垂径定理得BH=CH=
BE=2,再证明Rt△BAH∽Rt△BCA,利用相似比计算出AB=2
,然后在Rt△AED中利用勾股定理计算DE的长.
(2)作AH⊥BE,如图,根据垂径定理得BH=CH=
| 1 |
| 2 |
| 3 |
解答:(1)证明:∵四边形ABCD为平行四边形,
∴AB=CD,BC=AD,AB∥CD,∠B=∠ADC,
∵AB⊥AC,
∴AC⊥CD,
∴∠ACD=90°,
∵AD∥BC,
∴∠AEB=∠DAE,
∵AB=AE,
∴∠B=∠AEB,AE=DC,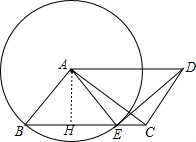
∴∠DAE=∠ADC,
在△AED和△DCA中,
,
∴△AED≌△DCA(SAS),
∴∠AED=∠DCA=90°,
∴AE⊥DE,
∴DE为⊙O的切线;
(2)解:作AH⊥BE,如图,
则BH=CH=
BE=2,
∵∠ABH=∠CBA,
∴Rt△BAH∽Rt△BCA,
∴
=
,即
=
,
∴AB=2
,
∴AE=2
,
在Rt△AED中,∵AD=BC=6,AE=2
,
∴DE=
=2
.
∴AB=CD,BC=AD,AB∥CD,∠B=∠ADC,
∵AB⊥AC,
∴AC⊥CD,
∴∠ACD=90°,
∵AD∥BC,
∴∠AEB=∠DAE,
∵AB=AE,
∴∠B=∠AEB,AE=DC,

∴∠DAE=∠ADC,
在△AED和△DCA中,
|
∴△AED≌△DCA(SAS),
∴∠AED=∠DCA=90°,
∴AE⊥DE,
∴DE为⊙O的切线;
(2)解:作AH⊥BE,如图,
则BH=CH=
| 1 |
| 2 |
∵∠ABH=∠CBA,
∴Rt△BAH∽Rt△BCA,
∴
| BA |
| BC |
| BH |
| BA |
| BA |
| 4+2 |
| 2 |
| BA |
∴AB=2
| 3 |
∴AE=2
| 3 |
在Rt△AED中,∵AD=BC=6,AE=2
| 3 |
∴DE=
| AD2-AE2 |
| 6 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了平行四边形的性质、勾股定理和相似三角形的判定与性质.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目

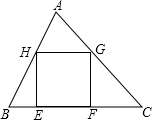 如图,在△ABC中,正方形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,BC=15cm,BC边上的高是10cm,求正方形的面积.
如图,在△ABC中,正方形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,BC=15cm,BC边上的高是10cm,求正方形的面积. 如图,OP是∠AOB内任意一条射线,OM平分∠AOP,ON平分∠POB,∠MON=60°,求∠AOB的度数.
如图,OP是∠AOB内任意一条射线,OM平分∠AOP,ON平分∠POB,∠MON=60°,求∠AOB的度数.