题目内容
已知一个四棱锥的正视图和俯视图如图所示，其中a+b=10，则该四棱锥体积的最大值为（ ）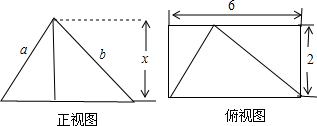
A、8
| ||
B、24
| ||
| C、16 | ||
| D、48 |
考点：由三视图判断几何体
专题：
分析：由三视图可知几何体是底面为长方形的四棱锥，求出底面面积和高，代入可得答案．
解答：解：如图：
由三视图可知，
S在底面射影在CD边上，即正视图等价于△SDC，
S点为以C、D为焦点椭圆上点，
则当a=b=5时，SE有最大值为4，
则V四棱锥=
×2×6×4=16．
故该四棱锥体积的最大值为16．
故选：C．
由三视图可知，
S在底面射影在CD边上，即正视图等价于△SDC，
S点为以C、D为焦点椭圆上点，
则当a=b=5时，SE有最大值为4，
则V四棱锥=
| 1 |
| 3 |
故该四棱锥体积的最大值为16．
故选：C．
点评：本题考查的是由三视图求体积，根据三视图得到几何体的形状是解答的关键．
练习册系列答案
相关题目
一件商品按成本价提高40%后标价，再打八折（标价的80%）销售，售价为240元．设这件商品的成本价为x元，根据题意，列方程正确的是（ ）
| A、x•40%×80%=240 |
| B、x（1+40%）×80%=240 |
| C、240×40×80%=x |
| D、x•40%=240×80% |
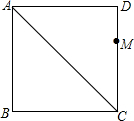作图题：线段AC是正方形ABCD的对角线，点M是边CD上的一定点（不与D、C重合），请在对角线AC上取一点P，使得△PDM的周长值最小，并作简要说明．
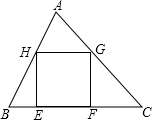如图，在△ABC中，正方形EFGH的两个顶点E、F在BC上，另两个顶点G、H分别在AC、AB上，BC=15cm，BC边上的高是10cm，求正方形的面积．