题目内容
13.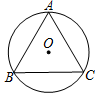 若⊙O是等边△ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为$2\sqrt{3}$.
若⊙O是等边△ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为$2\sqrt{3}$.
分析 首先连接OB,OC,过点O作OD⊥BC于D,由⊙O是等边△ABC的外接圆,即可求得∠OBC的度数,然后由三角函数的性质即可求得OD的长,又由垂径定理即可求得等边△ABC的边长.
解答 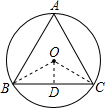 解:连接OB,OC,过点O作OD⊥BC于D,
解:连接OB,OC,过点O作OD⊥BC于D,
∴BC=2BD,
∵⊙O是等边△ABC的外接圆,
∴∠BOC=$\frac{1}{3}$×360°=120°,
∵OB=OC,
∴∠OBC=∠OCB=$\frac{180°-∠BOC}{2}$=$\frac{180°-120°}{2}$=30°,
∵⊙O的半径为2,
∴OB=2,
∴BD=OB•cos∠OBD=2×cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴BC=2BD=2$\sqrt{3}$.
∴等边△ABC的边长为2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查了垂径定理,圆的内接等边三角形,以及三角函数的性质等知识.此题难度不大,解题的关键是掌握数形结合思想的应用与辅助线的作法.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
5.下列等式成立的是( )
| A. | $\frac{2}{a}$+$\frac{3}{b}$=$\frac{5}{ab}$ | B. | $\frac{3}{3a+b}$=$\frac{1}{a+b}$ | C. | $\frac{ab}{ab-{b}^{2}}$=$\frac{a}{a-b}$ | D. | $\frac{a}{-a+b}$=-$\frac{a}{a+b}$ |
2.袋子中装有15个黑球、1个白球,它们除颜色外无其他差别,随机从袋子中摸出一个球,则下列说法正确的是( )
| A. | 这个球可能是白球 | |
| B. | 摸到黑球、白球的可能性的大小一样 | |
| C. | 这个球一定是黑球 | |
| D. | 事先能确定摸到什么颜色的球 |
 如图,已知AB⊥CD,EF⊥AB,∠DGC=105°,∠BCA=75°,请说明∠CEF+∠CDG=180°的理由.
如图,已知AB⊥CD,EF⊥AB,∠DGC=105°,∠BCA=75°,请说明∠CEF+∠CDG=180°的理由. 如图,DE⊥AC,∠AGF=∠ABC,∠GFB+∠BDE=180°,试判断BF与AC的位置关系,并说明理由.
如图,DE⊥AC,∠AGF=∠ABC,∠GFB+∠BDE=180°,试判断BF与AC的位置关系,并说明理由.
 将△ABC的纸片按如图所示的方式折叠,使点B落在边AC上,记为点B′,折叠痕为EF,已知AB=AC=8,BC=10,若以点B′、F、C为顶点的三角形与△ABC相似,那么BF的长度是$\frac{40}{9}$或5.
将△ABC的纸片按如图所示的方式折叠,使点B落在边AC上,记为点B′,折叠痕为EF,已知AB=AC=8,BC=10,若以点B′、F、C为顶点的三角形与△ABC相似,那么BF的长度是$\frac{40}{9}$或5.