题目内容
 已知∠ACB=90°,AC=BC,直线L过点C,AE⊥L,BF⊥L,P为AB中点,求证:PF=PE.
已知∠ACB=90°,AC=BC,直线L过点C,AE⊥L,BF⊥L,P为AB中点,求证:PF=PE.考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:连接CP,则AP=BP=CP,由∠ACB=90°,AE⊥L,BF⊥L,可得出∠ACE=∠CBF,从而可证得△ACE≌△CBF,所以有CE=BF,结合∠ACE=∠CBF,可得∠PCE=∠PBF,可证得△PCE≌△PBF,可得出结论.
解答: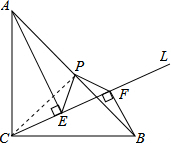 证明:连接CP,
证明:连接CP,
∵∠ACB=90°,AE⊥L,BF⊥L,
∴∠ACE+∠FCB=∠CBF+∠FCB,
∴∠ACE=∠CBF,PC=PB=PA,
在△ACE和△CBF中,
,
∴△ACE≌△CBF(AAS),
∴CE=BF,
∵∠ACP=∠CBP=45°,且∠ACP+∠PCE=∠CBP+∠PBF,
∴∠PCE=∠PBF,
在△PCE和△PBF中,
,
∴△PCE≌△PBF(SAS),
∴PE=PF.
 证明:连接CP,
证明:连接CP,∵∠ACB=90°,AE⊥L,BF⊥L,
∴∠ACE+∠FCB=∠CBF+∠FCB,
∴∠ACE=∠CBF,PC=PB=PA,
在△ACE和△CBF中,
|
∴△ACE≌△CBF(AAS),
∴CE=BF,
∵∠ACP=∠CBP=45°,且∠ACP+∠PCE=∠CBP+∠PBF,
∴∠PCE=∠PBF,
在△PCE和△PBF中,
|
∴△PCE≌△PBF(SAS),
∴PE=PF.
点评:本题主要考查三角形全等的判定和性质,寻找三角形全等的条件是证题的关键.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠B=90°,∠A=38°,AC的垂直平分线MN与AB交于D点,则∠BCD的度数是
如图,在Rt△ABC中,∠B=90°,∠A=38°,AC的垂直平分线MN与AB交于D点,则∠BCD的度数是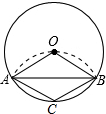 如图,将圆形纸片折叠后
如图,将圆形纸片折叠后
 如图,在直角坐标系中,平行四边形AOCD的边OC在x轴上,边AD与与y轴交与点H,点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),且∠OEF=∠A=∠DOC,CD=10,sin∠OCD=
如图,在直角坐标系中,平行四边形AOCD的边OC在x轴上,边AD与与y轴交与点H,点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),且∠OEF=∠A=∠DOC,CD=10,sin∠OCD= 如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=
如图,在Rt△ABC中,∠C=90°,∠A=30°,AC= 如图所示,CE⊥AB,BD⊥AC,BF=CF,求证:AF为∠BAC的平分线.
如图所示,CE⊥AB,BD⊥AC,BF=CF,求证:AF为∠BAC的平分线.