题目内容
已知抛物线y=ax2与四条直线x=1，x=2，y=1，y=2所围成的正方形有公共点，若a为整数，则a= ．
考点：二次函数的性质
专题：
分析：根据二次函数y=ax2的|a|越大开口越小，可得答案．
解答：解：当a＜0时，抛物线开口朝下，与正方形ABCD没有交点
∴a＞0，
所以y=ax2开口向上．
如图：
如果y=ax2在A点和C点之间的范围内，就会与正方形有公共点
当y=ax2经过A点时，12×a=2，解得a=2；
当y=ax2经过C点时，22×a=1，解得 a=0.25；
即0.25≤a≤2，
∴a=1或a=2，
故答案为：1或2．
∴a＞0，
所以y=ax2开口向上．
如图：
如果y=ax2在A点和C点之间的范围内，就会与正方形有公共点
当y=ax2经过A点时，12×a=2，解得a=2；
当y=ax2经过C点时，22×a=1，解得 a=0.25；
即0.25≤a≤2，
∴a=1或a=2，
故答案为：1或2．
点评：本题考查了二次函数的性质，利用了二次函数的性质．
练习册系列答案
相关题目
下列各对数互为相反数的是（ ）
| A、-（-8）与+（+8） |
| B、-（+8）与+|-8| |
| C、-（-8）与-（+7） |
| D、-|-8|与+（-8） |
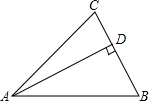在△ABC中，AD⊥BC于点D，∠BAC=45°，BD=3，DC=2，则△ABC的面积为
已知∠ACB=90°，AC=BC，直线L过点C，AE⊥L，BF⊥L，P为AB中点，求证：PF=PE．