题目内容
 如图,在Rt△ABC中,∠B=90°,∠A=38°,AC的垂直平分线MN与AB交于D点,则∠BCD的度数是
如图,在Rt△ABC中,∠B=90°,∠A=38°,AC的垂直平分线MN与AB交于D点,则∠BCD的度数是考点:线段垂直平分线的性质
专题:
分析:由AC的垂直平分线MN与AB交于D点,可得AD=CD,即可求得∠ACD的度数,又由在Rt△ABC中,∠B=90°,∠A=38°,即可求得∠ACB的度数,继而求得答案.
解答:解:∵AC的垂直平分线MN与AB交于D点,
∴AD=CD,
∴∠ACD=∠A=38°,
∵在Rt△ABC中,∠B=90°,∠A=38°,
∴∠ACB=90°-∠A=52°,
∴∠BCD=∠ACB-∠ACD=14°.
故答案为:14°.
∴AD=CD,
∴∠ACD=∠A=38°,
∵在Rt△ABC中,∠B=90°,∠A=38°,
∴∠ACB=90°-∠A=52°,
∴∠BCD=∠ACB-∠ACD=14°.
故答案为:14°.
点评:此题考查了线段垂直平分线的性质以及直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
下列各对数互为相反数的是( )
| A、-(-8)与+(+8) |
| B、-(+8)与+|-8| |
| C、-(-8)与-(+7) |
| D、-|-8|与+(-8) |
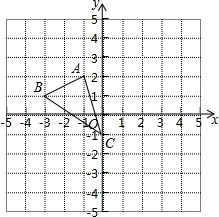 如图所示,已知△ABC.
如图所示,已知△ABC.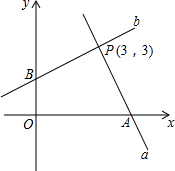 如图,相交于P(3,3)的互相垂直的两直线a、b中直线a与x轴正半轴交于点A,直线b与y轴正半轴交于点B.
如图,相交于P(3,3)的互相垂直的两直线a、b中直线a与x轴正半轴交于点A,直线b与y轴正半轴交于点B.
 已知∠ACB=90°,AC=BC,直线L过点C,AE⊥L,BF⊥L,P为AB中点,求证:PF=PE.
已知∠ACB=90°,AC=BC,直线L过点C,AE⊥L,BF⊥L,P为AB中点,求证:PF=PE.