题目内容
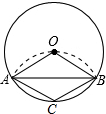 如图,将圆形纸片折叠后
如图,将圆形纸片折叠后 |
| AB |
 |
| AB |
考点:翻折变换(折叠问题)
专题:
分析:根据在同圆或等圆中等弧所对的弦相等可得AC=BC,再根据翻折的性质可得AC=AO,BC=BO,从而得到AC=BC=BO=AO,再根据四条边都相等的四边形是菱形解答.
解答:解:∵点C为
的中点,
∴AC=BC,
∵圆形纸片折叠后
恰好经过圆心O,
∴AC=AO,BC=BO,
∴AC=BC=BO=AO,
∴四边形ACBO是菱形.
故答案为:菱形.
 |
| AB |
∴AC=BC,
∵圆形纸片折叠后
 |
| AB |
∴AC=AO,BC=BO,
∴AC=BC=BO=AO,
∴四边形ACBO是菱形.
故答案为:菱形.
点评:本题考查了翻折变换的性质,菱形的判定,熟记翻折前后互相重合的线段相等是解题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
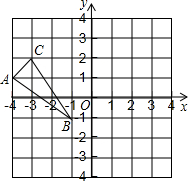 如图,△ABC三个顶点的坐标分别是A(-4,1),B(-1,-1),C(-3,2).
如图,△ABC三个顶点的坐标分别是A(-4,1),B(-1,-1),C(-3,2). 已知∠ACB=90°,AC=BC,直线L过点C,AE⊥L,BF⊥L,P为AB中点,求证:PF=PE.
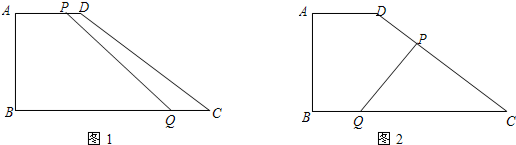
已知∠ACB=90°,AC=BC,直线L过点C,AE⊥L,BF⊥L,P为AB中点,求证:PF=PE. 已知∠B=∠C=90°,M是BC的中点,MN⊥AD,若∠1=∠2,求证:∠3=∠4,你还有什么发现?
已知∠B=∠C=90°,M是BC的中点,MN⊥AD,若∠1=∠2,求证:∠3=∠4,你还有什么发现?