��Ŀ����
12�����������κ�����ͼ�����ԭ��O���ĶԳƣ����������κ���Ϊ������ԭ�����ĶԳƶ��κ���������1����ֱ��д�����κ���y=2��x-1��2+3������ԭ�����ĶԳƶ��κ�����y��ĺ�������ʽ��
��2������1���еĶ��κ���y��y��ĺ���ֵͬʱ��x���������Сʱ����x��ȡֵ��Χ��
��3��������x���������κ���y1=axx2+b1x+c1��y2=a2x2+b2x+c2Ϊ������ԭ�����ĶԳƶ��κ���������֪a1=1������y3=y1+y2��ͼ���뺯��y4=$\frac{1}{2}$��y1-y2����ͼ���ڵ㣨1��2�����ԱȽ�y3��y4�Ĵ�С��
���� ��1���ѣ�-x��-y������y=2��x-1��2+3�����ɵõ�����ʽy�䣮
��2������ͼ�ɽ�����⣮
��3�������y3��y4�Ľ���ʽ������ͼ�ɽ�����⣮
��� �⣺��1�����κ���y=2��x-1��2+3������ԭ�����ĶԳƶ��κ�����y��ĺ�������ʽΪy��=-2����x+1��2-3��
��2����ͼ��ͼ���֪�����κ���y��y��ĺ���ֵͬʱ��x���������Сʱ��-1��x��1��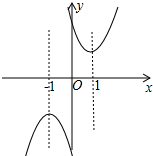
��3�������⣬a2=-1��b1=b2��c1=-c2��
��y3=y1+y2=2b1x��y4=$\frac{1}{2}$��y1-y2��=x2+c1��
�ߺ���y3=y1+y2��ͼ���뺯��y4=$\frac{1}{2}$��y1-y2����ͼ���ڵ㣨1��2����
��b1=1��c1=1��
��y3=2x��y4=x2+1��
����ͼ���֪��y4��y3��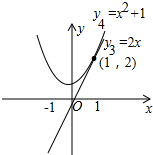 ��
��
���� ���⿼����κ����ۺ��⡢����Ĺؼ����������⣬ѧ�����ú���ͼ�������⣬ѧ��̽������ԭ�����ĶԳƵĶ��κ����Ľ���ʽ������������̽���õ����ɽ�����⣬�����п�ѹ���⣮

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ��������ÿ��С�����εı߳���Ϊ1���߶�AB���߶�EF�Ķ˵����С�����εĶ����ϣ�
��ͼ��������ÿ��С�����εı߳���Ϊ1���߶�AB���߶�EF�Ķ˵����С�����εĶ����ϣ� ��ͼ�������ο�ƬA�࣬B��ͳ����ο�ƬC�������ţ���Ҫ��A��B��C���Ƭƴһ����Ϊ��a+3b������Ϊ��a+b���ij����Σ�����ҪC�Ƭ��������
��ͼ�������ο�ƬA�࣬B��ͳ����ο�ƬC�������ţ���Ҫ��A��B��C���Ƭƴһ����Ϊ��a+3b������Ϊ��a+b���ij����Σ�����ҪC�Ƭ�������� ���������ſ�Ƭ���ֱ��������ο�ƬA��B�ͳ����ο�ƬC����Ƭ��С��ͼ��ʾ�����Ҫƴһ����Ϊ��3a+b������Ϊ��a+2b���Ĵ��Σ�����ҪC�Ƭ7�ţ�
���������ſ�Ƭ���ֱ��������ο�ƬA��B�ͳ����ο�ƬC����Ƭ��С��ͼ��ʾ�����Ҫƴһ����Ϊ��3a+b������Ϊ��a+2b���Ĵ��Σ�����ҪC�Ƭ7�ţ�