题目内容
14. 如图所示:点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+2|+|b-6|=0.
如图所示:点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+2|+|b-6|=0.(1)点A表示的数是-2,点B表示的数是6,线段AB的长度是8.
(2)若两动点A、B同时出发,分别以1单位长度/秒、3单位长度/秒的速度沿数轴向右、向左运动,求相遇时数轴上的点表示的数;
(3)若两动点A、B同时出发,分别以1单位长度/秒、3单位长度/秒的速度沿数轴的负方向运动,另有一动点C
从A点出发,以2单位长度/秒的速度在A、B两点之间作往返运动(即到达B点或A点后立即返回,掉头时间忽略不计),直到点B追上点A时点C停止运动.求点C从开始运动到停止运动,一共行驶了多少个单位长度?
分析 (1)利用非负数的性质得出a、b的数值即可;
(2)设运动t秒时,两点相遇,根据行驶的路程和为AB之间的距离列出方程求得t,再利用移动规律求得相遇时数轴上的点表示的数;
(3)设经过a秒点B追上点A,根据行驶的路程差为AB之间的距离列出方程求得a,进一步利用速度×时间得出一共行驶了多少个单位长度即可.
解答 解:(1)∵|a+2|+|b-6|=0
∴a=-2,b=6,
点A表示的数是-2,点B表示的数是6,线段AB的长度是8.
(2)设运动t秒时,两点相遇,由题意得
t+3t=8
解得:t=2,
相遇时数轴上的点表示的数-1+1×2=1;
(2)设经过a秒点B追上点A,由题意得
3a-a=8
解得:a=4,
则4×2=8.
答:一共行驶了8个单位长度.
点评 此题考查一元一次方程的实际运用,结合数轴,掌握行程问题中的基本数量关系是解决问题的关键.

练习册系列答案
相关题目
6.下列计算正确的是( )
| A. | $\frac{7}{10}$×$\frac{8}{5}$=1 | B. | $\frac{4}{5}$÷5=4 | C. | (4$+\frac{1}{2}$)×$\frac{3}{4}$=4×$\frac{3}{4}$$+\frac{1}{2}$ | D. | $\frac{2}{3}$÷2=$\frac{1}{3}$ |
4.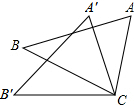 如图,△ACB≌△A′CB,点A和点A′,点B和点B′是对应点,∠BCB′=30°,则∠ACA′的度数为( )
如图,△ACB≌△A′CB,点A和点A′,点B和点B′是对应点,∠BCB′=30°,则∠ACA′的度数为( )
 如图,△ACB≌△A′CB,点A和点A′,点B和点B′是对应点,∠BCB′=30°,则∠ACA′的度数为( )
如图,△ACB≌△A′CB,点A和点A′,点B和点B′是对应点,∠BCB′=30°,则∠ACA′的度数为( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
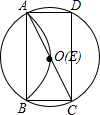 已知⊙O为矩形ABCD的外接圆,⊙O的半径为r,将劣弧沿弦AB翻折交AC于点E,连接BE.
已知⊙O为矩形ABCD的外接圆,⊙O的半径为r,将劣弧沿弦AB翻折交AC于点E,连接BE. 已知:如图,AB=AC,DB=DC,求证:∠B=∠C.
已知:如图,AB=AC,DB=DC,求证:∠B=∠C. 已知有理数a,b在数轴上如图所示,请你将a,-a,b,-b,0按从小到大的顺序排列-b<a<0<-a<b.
已知有理数a,b在数轴上如图所示,请你将a,-a,b,-b,0按从小到大的顺序排列-b<a<0<-a<b.