题目内容
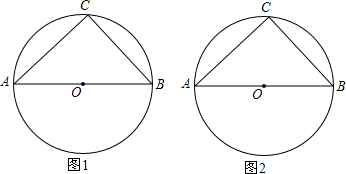
4.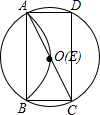 已知⊙O为矩形ABCD的外接圆,⊙O的半径为r,将劣弧沿弦AB翻折交AC于点E,连接BE.
已知⊙O为矩形ABCD的外接圆,⊙O的半径为r,将劣弧沿弦AB翻折交AC于点E,连接BE.(1)如图1,若点E与圆心O重合,AB=2$\sqrt{3}$,请直接写出r=2,此时△BCE的形状为等边三角形;
(2)如图2,若点E与圆心O不重合,∠BAC=35°,求∠ABE的度数.
分析 (1)如图1,过点O作OF⊥AB于F,由垂径定理得到AF=$\frac{1}{2}$AB=$\frac{1}{2}$×2$\sqrt{3}$=$\sqrt{3}$,根据翻折后点E与圆心O重合,得到OF=$\frac{1}{2}$r,然后根据勾股定理即可得到结论;
(2)如图2,连接BE,由AC是直径,得到∠ABC=90°,于是得到∠ACB=90°-∠BAC=90°-35°=55°,根据翻折的性质得,$\widehat{AB}$=$\widehat{AEB}$,根据圆周角定理得到∠ACB=∠BAC+∠ABE=∠BEC,于是得到结论.
解答 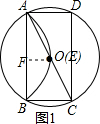 解:(1)如图1,过点O作OF⊥AB于F,
解:(1)如图1,过点O作OF⊥AB于F,
则AF=$\frac{1}{2}$AB=$\frac{1}{2}$×2$\sqrt{3}$=$\sqrt{3}$,
∵翻折后点E与圆心O重合,
∴OF=$\frac{1}{2}$r,
在Rt△AOE中,AO2=AF2+OF2,
即r2=($\sqrt{3}$)2+($\frac{1}{2}$r)2,
解得r=2,
∵OF=$\frac{1}{2}$AO,
∴∠BAC=30°,
∴∠ACB=60°,
∴△BCE是等边三角形;
故答案为:2,等边三角形;
(2)如图2,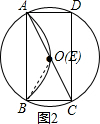 连接BE,
连接BE,
∵AC是直径,
∴∠ABC=90°,
∵∠BAC=35°,
∴∠ACB=90°-∠BAC=90°-35°=55°,
根据翻折的性质得,$\widehat{AB}$=$\widehat{AEB}$,
∴∠ACB=∠BAC+∠ABE=∠BEC,
∴∠ACB=∠BEC=55°,
∴∠ABE=90°-(180°-∠ACB-∠BEC)=20°.
点评 本题考查了垂径定理,勾股定理的应用,翻折的变换的性质,以及圆周角定理,(1)作辅助线构造出半径、半弦、弦心距为边的直角三角形是解题的关键,(2)根据同弧所对的圆周角相等求解是解题的关键.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
| A. | 数学式子 | B. | 表格 | C. | 图象 | D. | 函数 |
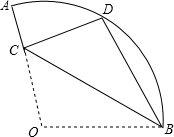 如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折线交OA于点C,则∠ABD=25°.
如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折线交OA于点C,则∠ABD=25°. 如图所示:点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+2|+|b-6|=0.
如图所示:点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+2|+|b-6|=0.