题目内容
7．把抛物线y=-2x2+4x-5向左平移3个单位后，它与y轴的交点是（0，-11）．分析 利用配方法将已知抛物线解析式转化为顶点式，然后得到平移后抛物线解析式，根据新解析式求解即可．
解答 解：y=-2x2+4x-5=-2（x-1）2-3，其顶点坐标是（1，-3），将其向左平移3个单位后的顶点坐标是（-2，-3），
故其抛物线解析式为：y=-2（x+2）2-3=-2x2-8x-11．
所以它与y轴的交点是（0，-11）．
故答案是：（0，-11）．
点评 本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
练习册系列答案
相关题目
17．下列四个命题中，正确的个数有（ ）
①圆的对称轴是直径；
②经过三点可以确定一个圆；
③三角形的外心到三角形各顶点的距离都相等；
④半径相等的两个半圆是等弧；
⑤平分弦的直径垂直于弦．
①圆的对称轴是直径；
②经过三点可以确定一个圆；
③三角形的外心到三角形各顶点的距离都相等；
④半径相等的两个半圆是等弧；
⑤平分弦的直径垂直于弦．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
2．已知点（-1，y1），（2，y2），$（{\sqrt{5}，{y_3}}）$在反比例函数y=-$\frac{{{k^2}+1}}{x}$的图象上，则下列关系式正确的是（ ）
| A． | y3＜y2＜y1 | B． | y2＜y3＜y1 | C． | y3＜y1＜y2 | D． | y2＜y1＜y3 |
如图，在平面直角坐标系内，已知点A（0，6），B（8，0），动点P从点A开始在线段AO上每秒1个单位长度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度向点A移动，设点P、Q移动的时间为t秒．
19．直线y=2x+6与x轴交点的坐标是（ ）
| A． | （0，-3） | B． | （0，3） | C． | （-3，0） | D． | （-$\frac{9}{2}$，1） |
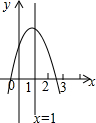二次函数y=ax2+bx+c（a，b是常数，a≠0）图象的对称轴是直线x=1，轴的交点坐标一个在-1和0之间，另一个交点在2和3之间，如图所示，对于下列说法：①ab＜0；②a-b+c＜0；③3a+c＜0；④当-1＜x＜3时，y＞0，其中正确的个数是 （ ）
17．相反数是2的数是（ ）
| A． | -2 | B． | $\frac{1}{2}$ | C． | 2 | D． | $-\frac{1}{2}$ |