题目内容
12. 如图,在平面直角坐标系内,已知点A(0,6),B(8,0),动点P从点A开始在线段AO上每秒1个单位长度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度向点A移动,设点P、Q移动的时间为t秒.
如图,在平面直角坐标系内,已知点A(0,6),B(8,0),动点P从点A开始在线段AO上每秒1个单位长度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度向点A移动,设点P、Q移动的时间为t秒.(1)求直线AB的解析式.
(2)当t为何值时,△APQ和△AOB相似.
(3)当t为何值时,△APQ的面积为$\frac{24}{5}$个平方单位.
分析 (1)根据点A(0,6),B(8,0),运用待定系数法求得直线AB的解析式;
(2)当△APQ和△AOB相似时,根据∠PAQ与∠BAO是公共角,分两种情况讨论,分别列比例式求解即可;
(3)先过点Q作QH⊥AO于H,并根据相似三角形的性质,用含t的代数式表示HQ,再根据△APQ的面积为$\frac{24}{5}$,列出关于t的一元二次方程,求得t的值即可.
解答 解:(1)设直线AB的解析式为y=kx+b,则
将点A(0,6),B(8,0)代入,可得
$\left\{\begin{array}{l}{6=b}\\{0=8k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=6}\end{array}\right.$
∴直线AB的解析式为y=-$\frac{3}{4}$x+6;
(2)由A(0,6),B(8,0)可得,AO=6,BO=8,
∴在直角三角形AOB中,AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵AP=t,BQ=2t,
∴AQ=10-2t,
∵∠PAQ=∠BAO,
∴分两种情况讨论:
①当△AOB∽△APQ时,$\frac{AP}{AO}$=$\frac{AQ}{QB}$,
即$\frac{t}{6}$=$\frac{10-2t}{10}$,
解得t=$\frac{30}{11}$;
②当△AOB∽△AQP时,$\frac{AP}{AB}$=$\frac{AQ}{AO}$,
即$\frac{t}{10}$=$\frac{10-2t}{6}$,
解得t=$\frac{50}{13}$,
综上,当t=$\frac{30}{11}$或$\frac{50}{13}$秒时,△APQ和△AOB相似;
(3)过点Q作QH⊥AO于H,则HQ∥OB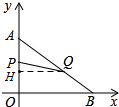 ,
,
∴$\frac{HQ}{OB}$=$\frac{AQ}{AB}$,
即$\frac{HQ}{8}$=$\frac{10-2t}{10}$,
解得HQ=8-$\frac{8}{5}$t,
∵△APQ的面积为$\frac{24}{5}$,
∴$\frac{1}{2}$×AP×QH=$\frac{24}{5}$,
即$\frac{1}{2}$×t×(8-$\frac{8}{5}$t)=$\frac{24}{5}$,
解得t1=2,t2=3,
∴当t=2或3秒时,△APQ的面积为$\frac{24}{5}$个平方单位.
点评 本题主要考查了相似三角形的综合运用,当两个三角形相似时,若没有规定对应顶点,则需要分情况讨论.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,构造相似三角形的一般方法是通过作平行线.

| A. | 1 | B. | 0 | C. | 2或-2 | D. | $\frac{1}{2}$ |

| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 2$\sqrt{3}$ |
| A. | 有一组邻边相等的四边形是菱形 | |
| B. | 有一个角是直角的平行四边形是矩形 | |
| C. | 有一组对边平行的四边形是平行四边形 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
| A. | 1.73×102 | B. | 17.3×104 | C. | 1.73×105 | D. | 0.173×104 |
| A. | $\sqrt{81}$=±9 | B. | -$\sqrt{3.6}$=-0.6 | C. | $\sqrt{(-10)^{2}}$=-10 | D. | $\root{3}{-5}$=-$\root{3}{5}$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |