题目内容
3.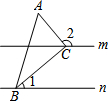 如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2的度数为( )
如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2的度数为( )| A. | 140° | B. | 130° | C. | 120° | D. | 110° |
分析 先根据平行线的性质求出∠3的度数,再由∠ACB=90°得出∠4的度数,根据补角的定义即可得出结论.
解答  解:∵m∥n,∠1=40°,
解:∵m∥n,∠1=40°,
∴∠3=∠1=40°.
∵∠ACB=90°,
∴∠4=∠ACB-∠3=90°-40°=50°,
∴∠2=180°-∠4=180°-50°=130°.
故选B.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.

练习册系列答案
相关题目
13. 如图,正方形ABCD中,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )
如图,正方形ABCD中,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )
 如图,正方形ABCD中,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )
如图,正方形ABCD中,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )| A. | 64 | B. | 72 | C. | 76 | D. | 84 |
11. 如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,则∠E=( )
如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,则∠E=( )
 如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,则∠E=( )
如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,则∠E=( )| A. | 90° | B. | 45° | C. | 30° | D. | 22.5° |
18. 如图,经过平移能得到如图图形的是( )
如图,经过平移能得到如图图形的是( )
 如图,经过平移能得到如图图形的是( )
如图,经过平移能得到如图图形的是( )| A. |  | B. |  | C. |  | D. |  |
12.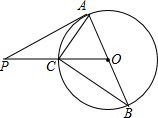 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )
 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )| A. | 3$\sqrt{3}$ | B. | 4 | C. | 5 | D. | 6 |
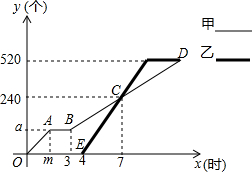 甲、乙两人各自加工相同数量的零件,甲先开始工作,中途因故停机检修1小时,重新工作时依旧按照原来的工作效率加工零件,如图是甲、乙两人在整个过程中各自加工的零件个数y(个)与甲工作时间x(时)之间的函数图象.
甲、乙两人各自加工相同数量的零件,甲先开始工作,中途因故停机检修1小时,重新工作时依旧按照原来的工作效率加工零件,如图是甲、乙两人在整个过程中各自加工的零件个数y(个)与甲工作时间x(时)之间的函数图象.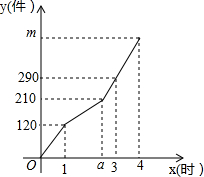 某工厂甲、乙两个车间同时开始生产某种产品,产品总任务量为m件,开始甲、乙两个车间工作效率相同.乙车间在生产一段时间后,停止生产,更换新设备,之后工作效率提高.甲车间始终按原工作效率生产.甲、乙两车间生产的产品总件数y与甲的生产时间x(时)的函数图象如图所示.
某工厂甲、乙两个车间同时开始生产某种产品,产品总任务量为m件,开始甲、乙两个车间工作效率相同.乙车间在生产一段时间后,停止生产,更换新设备,之后工作效率提高.甲车间始终按原工作效率生产.甲、乙两车间生产的产品总件数y与甲的生产时间x(时)的函数图象如图所示.