题目内容
14.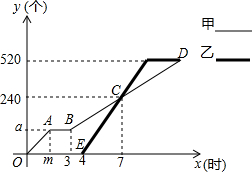 甲、乙两人各自加工相同数量的零件,甲先开始工作,中途因故停机检修1小时,重新工作时依旧按照原来的工作效率加工零件,如图是甲、乙两人在整个过程中各自加工的零件个数y(个)与甲工作时间x(时)之间的函数图象.
甲、乙两人各自加工相同数量的零件,甲先开始工作,中途因故停机检修1小时,重新工作时依旧按照原来的工作效率加工零件,如图是甲、乙两人在整个过程中各自加工的零件个数y(个)与甲工作时间x(时)之间的函数图象.(1)图中m=2,a=80.
(2)求重新工作后甲加工的零件个数y与x之间的函数关系式.
(3)求乙工作期间两人加工的零件个数相差100个时x的值.
分析 (1)根据题意列方程即可得到结论;
(2)设y与x之间的函数关系式为y=kx+b,列方程组即可得到结论;
(3)设直线CE的函数关系式为y=kx+b,求得直线CE的函数关系式为y=80x-320,根根据题意列方程即可得到结论.
解答 解:(1)m=3-1=2,
根据题意得:$\frac{a}{2}$=$\frac{240-a}{7-3}$,
解得:a=80.
故答案为:2,80;
(2)设y与x之间的函数关系式为y=kx+b,
∴$\left\{\begin{array}{l}{80=3k+b}\\{240=7k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=40}\\{b=-40}\end{array}\right.$,
∴y与x之间的函数关系式为y=40x-40;
(3)设直线CE的函数关系式为y=kx+b,
∴$\left\{\begin{array}{l}{0=4k+b}\\{240=7k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=80}\\{b=-320}\end{array}\right.$,
∴直线CE的函数关系式为y=80x-320,
根据题意得:(80x-320)-(40x-40)=100,
解得:x=$\frac{9}{2}$=4.5,或x=$\frac{19}{2}$=9.5.
答:乙工作期间两人加工的零件个数相差100个时x的值是4.5小时或9.5小时.
点评 本题主要考查用一次函数研究实际问题,具备在直角坐标系中的读图能力,并用待定系数法求一次函数关系式的简单运算.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
4.下列运算中,不正确的是( )
| A. | a8•a2=a10 | B. | a6÷a2=a4 | C. | (a2)3=a6 | D. | (-3a2b4)3=-27a6b7 |
2.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (ab)2=ab2 | C. | 2a4×3a5=6a9 | D. | (a2)3=a5 |
9.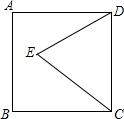 如图,正方形ABCD的边长为6,以CD为一边作等边三角形△DCE,点E在正方形内部,则点E到CD的距离是( )
如图,正方形ABCD的边长为6,以CD为一边作等边三角形△DCE,点E在正方形内部,则点E到CD的距离是( )
 如图,正方形ABCD的边长为6,以CD为一边作等边三角形△DCE,点E在正方形内部,则点E到CD的距离是( )
如图,正方形ABCD的边长为6,以CD为一边作等边三角形△DCE,点E在正方形内部,则点E到CD的距离是( )| A. | 6 | B. | 3$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
6.下列运算正确的是( )
| A. | (ab)3=a3b | B. | (a+b)2=a2+b2 | C. | a6÷a2=a3 | D. | π0=1 |
3.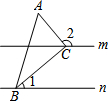 如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2的度数为( )
如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2的度数为( )
 如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2的度数为( )
如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2的度数为( )| A. | 140° | B. | 130° | C. | 120° | D. | 110° |
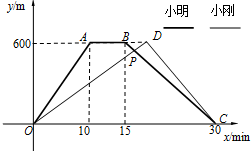 小明和小刚同时从公园门口出发,散步到公园“雨花亭”.他们离公园门口的距离y(m)与小刚行走的时间x(min)之间的关系如图.请根据图象回答:
小明和小刚同时从公园门口出发,散步到公园“雨花亭”.他们离公园门口的距离y(m)与小刚行走的时间x(min)之间的关系如图.请根据图象回答: