题目内容
 如图,等边三角形ABC中,AB=4,D是直线BC上一点,将△ABD绕点A逆时针旋转60°得到△ACE,若△BCE的面积为
如图,等边三角形ABC中,AB=4,D是直线BC上一点,将△ABD绕点A逆时针旋转60°得到△ACE,若△BCE的面积为| 3 |
考点:旋转的性质
专题:计算题
分析:作EH⊥BC于H,如图,根据等边三角形的性质得BC=AB=4,∠ABC=∠ACB=60°,再利用旋转的性质得∠ACE=∠ABD=60°,CE=BD,利用平角定义可计算出∠ECH=60°,再根据三角形面积公式求出EH=
,然后在Rt△CEH中,利用∠ECH的正弦可求出CE=1,则BD=1,于是CD=BC-BD=3.
| ||
| 2 |
解答:解: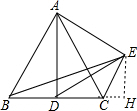 作EH⊥BC于H,如图,
作EH⊥BC于H,如图,
∵△ABC为等边三角形,
∴BC=AB=4,∠ABC=∠ACB=60°,
∵△ABD绕点A逆时针旋转60°得到△ACE,
∴∠ACE=∠ABD=60°,CE=BD,
∴∠ECH=180°-∠ACB-∠ACE=60°,
∵△BCE的面积为
,
∴
•BC•EH=
,即
×4×EH=
,解得EH=
,
在Rt△CEH中,∵sin∠ECH=
,
∴CE=
=1,
∴BD=1,
∴CD=BC-BD=4-1=3.
故答案为3.
 作EH⊥BC于H,如图,
作EH⊥BC于H,如图,∵△ABC为等边三角形,
∴BC=AB=4,∠ABC=∠ACB=60°,
∵△ABD绕点A逆时针旋转60°得到△ACE,
∴∠ACE=∠ABD=60°,CE=BD,
∴∠ECH=180°-∠ACB-∠ACE=60°,
∵△BCE的面积为
| 3 |
∴
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
在Rt△CEH中,∵sin∠ECH=
| EH |
| CE |
∴CE=
| ||||
| sin60° |
∴BD=1,
∴CD=BC-BD=4-1=3.
故答案为3.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的性质和解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,CD平分∠ACB,DE⊥AC于点E,DF⊥BC于点F,S△ABC=7,DE=2,AC=3,则BC的长是( )
如图,在△ABC中,CD平分∠ACB,DE⊥AC于点E,DF⊥BC于点F,S△ABC=7,DE=2,AC=3,则BC的长是( )
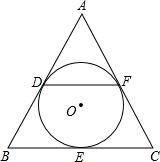 如图,△ABC的内切圆⊙O分别和AB,BC,CA切于点D,E,F,∠A=60°,BC=6,△ABC的周长为18,则DF的长为
如图,△ABC的内切圆⊙O分别和AB,BC,CA切于点D,E,F,∠A=60°,BC=6,△ABC的周长为18,则DF的长为

 如图,已知⊙0的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则么∠P等于
如图,已知⊙0的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则么∠P等于