Question

已知Rt△ABC，∠BAC=90°，∠C=30°，BC=8cm，将Rt△ABC绕点A顺时针旋转90°．后得到Rt△ADE（如图1）．
（Ⅰ）将Rt△ABC绕点A顺时针旋转得到Rt△AB₁C₁．AC₁交DE于点F，当△AEF为等腰三角形时，旋转角的度数为

 

；
（Ⅱ）将Rt△DAE沿AB方向平移，得到Rt△D₂A₂E₂（如图3），E₂D₂交AC于点P．A₂D₂交BC于点N，当NP∥AB时，平移距离为

 

cm．

Answer 1

考点：旋转的性质,平移的性质

专题：计算题

分析：（Ⅰ）由于Rt△ABC绕点A顺时针旋转90°后得到Rt△ADE，如图1，根据旋转的性质得∠E=∠C=30°，∠CAE=90°，∠DAE=∠BAC=90°，再由△ABC绕点A顺时针旋转得到△AB₁C₁，如图2，根据旋转的性质得∠CAC₁等于旋转角，然后分类讨论：当FA=FE时，根据等腰三角形的性质得∠EAF=∠E=30°，则利用互余可计算出∠CAC₁=60°；当EA=EF时，则∠EAF=∠EFA，利用三角形内角和可计算出∠EAF=

1

2

（180°-∠E）=75°，则∠CAC₁=90°-∠EARF=15°，于是得到旋转角的度数为15°或60°；
（Ⅱ）如图3，在Rt∠BAC中，根据含30度的直角三角形三边的关系得AB=

1

2

BC=4cm，AC=

3

AB=4

3

cm，再由旋转的性质得AE=AC=4

3

cm，接着根据平移的性质得A₂E₂=AE=4

3

cm，∠D₂A₂E₂=∠DAE=90°，∠A₂E₂D₂=∠E=30°，然后证明四边形AA₂NP为矩形得到NA₂=PA，设AA₂=x，则A₂B=AB-AA₂=4-x，AE₂=A₂E₂-AA₂=4

3

-x，在Rt△A₂BN中计算出NA₂=

3

A₂B=

3

（4-x），在Rt△AE₂P中计算出PA=

3

3

AE₂=

3

3

（4

3

-x），则

3

（4-x）=

3

3

（4

3

-x），解得x=6-2

3

，于是得到Rt△DAE沿AB方向平移，平移距离为（6-2

3

）cm．

解答：解：（Ⅰ）∵Rt△ABC绕点A顺时针旋转90°后得到Rt△ADE，如图1，
∴∠E=∠C=30°，∠CAE=90°，∠DAE=∠BAC=90°，
∴点D在AC上，
∵△ABC绕点A顺时针旋转得到△AB₁C₁，如图2，
∴∠CAC₁等于旋转角，
当FA=FE时，则∠EAF=∠E=30°，
∴∠CAC₁=90°-∠EAF=60°；
当EA=EF时，则∠EAF=∠EFA，
∵∠E=30°，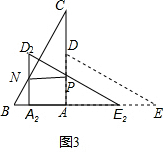
∴∠EAF=

1

2

（180°-30°）=75°，
∴∠CAC₁=90°-∠EARF=15°，
∴旋转角的度数为15°或60°；
（Ⅱ）如图3，
∵∠BAC=90°，∠C=30°，BC=8cm，
∴AB=

1

2

BC=4cm，AC=

3

AB=4

3

cm，
∵Rt△ABC绕点A顺时针旋转90°．后得到Rt△ADE，
∴AE=AC=4

3

cm，
∵Rt△DAE沿AB方向平移，得到Rt△D₂A₂E₂，
∴A₂E₂=AE=4

3

cm，∠D₂A₂E₂=∠DAE=90°，∠A₂E₂D₂=∠E=30°，
∵PN∥AB，
∴四边形AA₂NP为矩形，
∴NA₂=PA，
设AA₂=x，则A₂B=AB-AA₂=4-x，AE₂=A₂E₂-AA₂=4

3

-x，
在Rt△A₂BN中，∵∠B=60°，
∴NA₂=

3

A₂B=

3

（4-x），
在Rt△AE₂P中，∵∠AE₂P=30°，
∴PA=

3

3

AE₂=

3

3

（4

3

-x），
∴

3

（4-x）=

3

3

（4

3

-x），解得x=6-2

3

，
∴Rt△DAE沿AB方向平移，平移距离为（6-2

3

）cm．
故答案为：15°或60°；（6-2

3

）．

点评：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了平移的性质、等腰三角形的性质和解直角三角形．