题目内容
2.在△ABC中,AB=AC,AB的中垂线与AC所在直线相交所得的锐角为60度,则底角为15°或75°度.分析 根据题意画出图形,由DE是AB的中垂线,可得DE⊥AB,根据等腰三角形的性质可得∠ABC=∠C,又由AB的中垂线与AC所在的直线相交所得的锐角为60°,即可求得答案.
解答  解:∵DE是AB的中垂线,
解:∵DE是AB的中垂线,
∴DE⊥AB,
∵AB=AC,
∴∠ABC=∠C,
如图1,∵∠ADE=60°,
∴∠A=30°,
∴∠ABC=∠C=$\frac{180°-∠A}{2}$=75°;
如图2,∵∠ADE=60°,
∴∠DAE=30°,
∴∠B=$\frac{1}{2}$∠DAE=15°;
∴底角的度数为:15°或75°.
故答案为:15°或75°.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质,掌握等腰三角形的两个底角相等是解题的关键,注意掌握数形结合思想与分类讨论思想的应用.

练习册系列答案
相关题目
12.下列哪个点在直线y=-2x+3上( )
| A. | (-2,-7) | B. | (-1,1) | C. | (2,1) | D. | (-3,9) |
10.在△ABC中,∠C=90°,若AC=3,BC=5,则AB等于( )
| A. | $\sqrt{34}$ | B. | 4 | C. | $\sqrt{20}$ | D. | 都不对 |
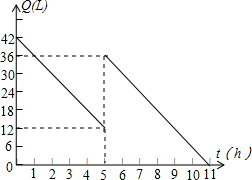 某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题:
某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题: