Question

5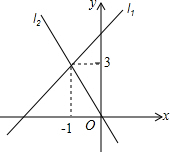．直线l₁：y=k₁x+b与直线l₂：y=k₂X在同一平面直角坐标系中的图象如图所示，则关于x、y的方程组$\left\{\begin{array}{l}y={k_1}x+b\\ y={k_2}x\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$．

Answer 1

分析 点（-1，3）是两个函数图象的交点，同时满足函数解析式；即同时是函数解析式以及方程组的公共解，则关于x、y的二元一次方程组解即可求出．

解答 解：因为函数图象交点坐标为两函数解析式组成的方程组的解．
因此方程组$\left\{\begin{array}{l}y={k_1}x+b\\ y={k_2}x\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$，
故答案为$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$

点评 本题考查了一次函数与二元一次方程组的知识，方程组的解就是使方程组中两个方程同时成立的一对未知数的值，而这一对未知数的值也同时满足两个相应的一次函数式，因此方程组的解就是两个相应的一次函数图象的交点坐标．